Πού πήγε η ενέργεια που χάθηκε; (Προσέξτε το θέμα αυτό!)

Απορία μαθητή. Μου δόθηκε η εξής άσκηση:

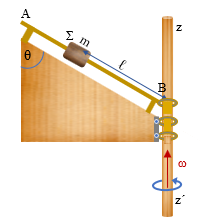
Η ράβδος του σχήματος είναι οριζόντια και μπορεί να στρέφεται γύρω από κατακόρυφο άξονα που διέρχεται από το μέσον της. Το μήκος της ράβδου είναι L και η μάζα της Μ. Σε απόσταση r από τον άξονα περιστροφής βρίσκονται δύο μεταλλικοί δακτύλιοι μάζας m, ο καθένας, που συνδέονται μεταξύ τους με ένα νήμα. Το σύστημα στρέφεται γύρω από τον άξονα με γωνιακή συχνότητα ω₀. Κάποια στιγμή το νήμα σπάει και οι δακτύλιοι, λόγω αδράνειας, ωθούνται στα άκρα της ράβδου, όπου δεν υπάρχει κανένα εμπόδιο να τους συγκρατήσει κι έτσι πέφτουν στο έδαφος. Να υπολογίστε τη γωνιακή ταχύτητα του συστήματος και την κινητική ενέργεια περιστροφής του, τη στιγμή που οι δύο δακτύλιοι φτάνουν στο τέλος της ράβδου. Η ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το κέντρο μάζας της είναι  I_ρ = ML²/12.

Γνωρίζω ότι πρέπει να χρησιμοποιήσω την αρχή διατήρησης στροφορμής:

                                         Ι₀ω₀ = Ι_τελω_τελ (=L) →  ω_τελ = Ι₀ω₀/Ι_τελ

Και επομένως: 

                                             ΔΚ_σροφ =  (1/2)Lω_τελ - (1/2)Lω₀ < 0,

δηλαδή, έχουμε απώλεια ενέργειας.

Έχω όμως τις εξής απορίες:

1. Δεν έχουμε εξωτερικές δυνάμεις και ροπές στο σύστημα. Γιατί παραβιάζεται εδώ η αρχή διατήρησης της ενέργειας:

                                                       (1/2)Ι₀ω₀² =  (1/2)Ι_τελω_τελ²

Απ’ όπου προκύπτει αποτέλεσμα:  ω_τελ = ω₀√( Ι₀/Ι_τελ) < ω₀  και ΔΚ = 0, εντελώς διαφορετικό; Πού πήγε η ενέργεια που χάθηκε;

2. Όταν οι δακτύλιοι φύγουν από τη ράβδο, η νέα της γωνιακή ταχύτητα θα υπολογιστεί από τη σχέση 

                                           Ι_ρ· ω_νεα = (Ι_ρ+ 2mL²/4) ω_τελ;

Είναι μια όμορφη απορία, που απ' την εμπειρία μου γνωρίζω ότι την έχουν και άλλοι μαθητές. 

Ας πάρουμε ένα-ένα τα ερωτήματα:

1. Δεν παραβιάζεται η αρχή διατήρησης της μηχανικής ενέργειας!

Στην εξίσωσή σου  (1/2)Ι₀ω₀² =  (1/2)Ι_τελω_τελ²,  θεωρείς ότι το σύστημα, τόσο στην αρχική όσο και στην τελική του κατάσταση, έχει μόνο κινητική ενέργεια λόγω περιστροφής. Όμως, υπάρχει και μια ποσότητα κινητικής ενέργειας  λόγω μεταφορικής κίνησης των δακτυλίων, καθώς αυτοί οδηγούνται, λόγω αδράνειας, προς τα άκρα της ράβδου. Οι δακτύλιοι, και περιστρέφονται και μετατοπίζονται, κι έτσι η συνολική τους ταχύτητα δεν είναι ίδια με την ταχύτητα των σημείων της ράβδου πάνω στα οποία εφάπτονται.

Πρέπει λοιπόν να διορθωθεί η προηγούμενη σχέση στην εξής

                                    (1/2)Ι₀ω₀² =  (1/2)Ι_τελω_τελ²+ 2(1/2)mυ_δ²    (1)

Όπου υ_δ είναι η ταχύτητα λόγω μεταφορικής κίνησης με την οποία φτάνουν οι δακτύλιοι στα άκρα της ράβδου.

Έτσι, στην εξίσωση (1) της Α.Δ.Μ.Ε υπάρχουν δύο άγνωστοι, το ω_τελ και η υ_δ και άρα, αφού το σύστημα είναι μονωμένο, πρέπει να καταφύγεις και σε μια άλλη αρχή διατήρησης, αυτή της Α.Δ.Σ   (Ι₀ω₀ = Ι_τελω_τελ), απ’ όπου άμεσα προκύπτει το ω_τελ. Ύστερα, από την εξίσωση (1), μπορείς να υπολογίσεις και την (ακτινική) ταχύτητα  με την οποία φτάνουν οι δακτύλιοι στα άκρα της ράβδου.

2.  Όχι. Όταν οι δακτύλιοι εγκαταλείψουν τη ράβδο, αυτή θα συνεχίσει να κινείται με γωνιακή ταχύτητα ω_τελ, (ίση με αυτήν που είχε το σύστημα, τη στιγμή που οι δακτύλιοι έφταναν στα άκρα της ράβδου).

Η εξήγηση είναι απλή:  Μπορεί οι δακτύλιοι να εγκαταλείπουν τη ράβδο, κρατάνε ίδια όμως τη στροφορμή τους, αφού δεν δέχονται κάποια εξωτερική ροπή. Πρέπει όμως να κρατήσει ίδια τη στροφορμή της και η ράβδος, αφού το σύστημα είναι μονωμένο, και αυτό σημαίνει ότι δε θα αλλάξει η γωνιακή της ταχύτητα.  

Στη σχέση, που γράφεις, έχεις παραλείψει τη στροφορμή που έχουν οι δακτύλιοι όταν εγκαταλείψουν τη ράβδο. Πρέπει να διορθωθεί στην εξής:

                         Ι_ρ· ω_νεα + (2mL²/4) ω_τελ = (Ι_ρ+2mL²/4) ω_τελ 

Είναι φανερό ότι από αυτήν προκύπτει ω_νεα = ω_τελ.

Παρατήρηση: Υπόψη ότι, επειδή το σύστημα είναι μονωμένο, δεν συνεπάγεται ότι έχουμε και διατήρηση της μηχανικής του ενέργειας. Αυτό ισχύει μόνο αν οι δυνάμεις μέσα σε αυτό είναι συντηρητικές.  Υπάρχει, για παράδειγμα, η άσκηση 4.60 του σχολικού βιβλίου. Εκεί οι δακτύλιοι σταματάνε στα εμπόδια που υπάρχουν στα δύο άκρα της ράβδου. Είναι φανερό ότι στην άσκηση αυτή δεν ισχύει η Α.Δ.Μ.Ε, αφού οι δακτύλιοι συγκρούονται με τα εμπόδια και θεωρούμε ότι παραμένουν εκεί (πλαστική κρούση). Όλη η κινητική τους ενέργεια λόγω της ακτινικής τους ταχύτητας μετατρέπεται σε θερμική. Όταν όμως το σύστημα είναι μονωμένο, ισχύει πάντα η αρχή διατήρησης της στροφορμής του.

Αβαρής ράβδος και δύο σφαιρίδια σε σύνθετη κίνηση

Η κινητική ενέργεια του συστήματος «αβαρής ράβδος – σφαιρίδια», που κινείται με ταχύτητα 5 m/s και εκτελεί 1 περιστροφή το δευτερόλεπτο γύρω από το κέντρο μάζας του, είναι:

   α. 650 J,     

   β. 316,67 J,    

   γ.  350 J

Επιλέξτε το σωστό και αιτιολογείστε.

Τρεις κύλινδροι

Τρεις παρόμοιοι συμπαγείς και ομογενείς κύλινδροι και ένα αβαρές σχοινί αποτελούν το σύστημα του σχήματος. Όταν κύλινδρος 3 κατεβαίνει, ο 1 κυλίεται χωρίς ολίσθηση πάνω στην οριζόντια επιφάνεια ενός τραπεζιού και το σχοινί, χωρίς να ολισθαίνει, θέτει σε περιστροφή τον κύλινδρο 2. 

Ράβδος με διαφορετικές ταχύτητες στα άκρα της

Στο σχήμα φαίνονται, κάποια χρονική στιγμή t₁, οι ταχύτητες των άκρων μιας ομογενούς ράβδου η οποία κινείται πάνω σε λείο οριζόντιο επίπεδο. Το μήκος της ράβδου είναι 1 m και η μάζα της 3 kg.

Να βρείτε:

α. Την κινητική ενέργεια της ράβδου

Από την ταχύτητα ολίσθησης στην ταχύτητα κύλισης

Μια μπάλα, που αρχικά ηρεμεί σε οριζόντιο επίπεδο, δέχεται μια στιγμιαία ώθηση και ξεκινάει με ταχύτητα υ₀ = 2,1 m/s, χωρίς αρχικά να κυλίεται (που σημαίνει ότι αρχικά κινείται ολισθαίνοντας στο έδαφος).  Επειδή όμως η τριβή ολίσθησης ανάμεσα στην μπάλα και στο έδαφος ασκεί μια ροπή πάνω της, η μπάλα θα αρχίσει να περιστρέφεται και τελικά η γωνιακή της ταχύτητα θα πάρει τέτοια τιμή, ώστε η μπάλα θα πάψει να γλιστράει.

Κίνηση σφαίρας σε ημισφαίριο

Μια σφαίρα, μάζας m = 1 kg και ακτίνας r = 0,1 m συγκρατείται αρχικά στη θέση που φαίνεται στο σχήμα. Κάποια στιγμή αφήνεται ελεύθερη (χωρίς να την σπρώξουμε).

α. Η σφαίρα κυλίεται στο κοίλο ημισφαιρικό δοχείο, ακτίνας R = 1,1 m, του σχήματος χωρίς να ολισθαίνει. Με πόση ταχύτητα διέρχεται από το χαμηλότερο σημείο Β του δοχείου;

β. Αν στη συνέχεια (μετά το σημείο Β) η εσωτερική επιφάνεια του δοχείου είναι λεία, να εξετάσετε, χωρίς υπολογισμούς:

Ρυμούλκηση (Μια "εύκολη" και μια "εκκεντρική")

1. Ένα βαγόνι τραίνου (η … εύκολη)

Ένα βαγόνι τραίνου, φορτωμένο με αυτοκίνητα, έχει μάζα 6000 kg και ρυμουλκείται σε ένα λείο ανηφορικό δρόμο με κλίση 1:30 (ημθ = 1/30), με τη βοήθεια ενός σχοινιού, που τυλίγεται χωρίς να γλιστράει γύρω από ένα κυλινδρικό τύμπανο με διάμετρο 1 m και ροπή αδράνειας 200 kg·m².

Στο τύμπανο ενεργεί σταθερή ροπή τ = 3000 Ν·m και περιστρέφεται γύρω από τον άξονά του, ο οποίος είναι ακλόνητα στερεωμένος, χωρίς τριβές, με σταθερή γωνιακή επιτάχυνση.

2. Μια μαρμάρινη κυλινδρική κολώνα (η … εκκεντρική)

Στη δεύτερη αυτή άσκηση ρυμουλκείται, όπως φαίνεται στο σχήμα, μια ομογενής μαρμάρινη κυλινδρική κολώνα, όπως  πριν, με τις εξής αλλαγές και προσθήκες:

i. Ο δρόμος δεν είναι λείος και ο κύλινδρος κυλίεται χωρίς να ολισθαίνει.

ii. Η κολώνα έχει μάζα Μ = 6000 kg, ακτίνα R₁ = 0,5 m και ροπή αδράνειας Ι₁ = 750 kg·m², ως προς τον γεωμετρικό της άξονα.

Η δύναμη από το σχοινί ενεργεί στο κέντρο μάζας του κυλίνδρου, κάθετα στον άξονα, και παράλληλα προς το δρόμο. Όλα τα άλλα μεγέθη είναι ίδια.

Η απάντηση στο παράδοξο της συνολικής στροφορμής δύο δίσκων

Δεν έχουμε εδώ διατήρηση της στροφορμής του συστήματος των δύο δίσκων. Αν ίσχυε, θα είχαμε: Ι₁ω₀ = Ι₁ω₁ – Ι₂ω₂, δηλαδή Ι₁ω₁ = Ι₁ω₀ + Ι₂ω₂, οπότε ω₁ > ω₀ και άρα η κινητική ενέργεια κάθε δίσκου θα αύξαινε, άρα και του συστήματος. Φυσικά, αυτό αντίκειται στην Α.Δ.Ε. συστήματος.

Τι συμβαίνει λοιπόν; 

Κοιτάξτε το αριστερό σχήμα (α): Θεωρήστε τους δύο δίσκους πάνω σε λείο οριζόντιο επίπεδο. Είναι η στιγμή που φέρνουμε σε επαφή τις περιφέρειες των  δύο δίσκων. Έχουν σχεδιαστεί οι δύο τριβές ολίσθησης (με κόκκινο χρώμα) στις περιφέρειες των δύο δίσκων. Είναι δύο δυνάμεις αντίθετες (δράση – αντίδραση), που δρουν στα σημεία επαφής των περιφερειών των δύο δίσκων. Επειδή οι εξωτερικές δυνάμεις, βάρος -  αντίδραση δαπέδου, έχουν συνισταμένη μηδέν, κάθε δίσκος δέχεται μια καθαρή δύναμη Τ, που παρουσιάζει ροπή ως προς το κέντρο μάζας του. Το αποτέλεσμα είναι γνωστό: Ο δίσκος 2 θα εκτελέσει μια σύνθετη κίνηση, μεταφορική κατά τη διεύθυνση της Τ και στροφική γύρω από το κέντρο μάζας του, κατά τη φορά της ροπής της Τ. Αντίστοιχα, ο δίσκος 1 θα εκτελέσει και αυτός μια μεταφορική κίνηση κατά τη φορά της Τ, ενώ η στροφική κίνηση θα περιοριστεί και θα μειωθεί (λόγω της ροπής της Τ) η γωνιακή του ταχύτητα. Έτσι, σε ελάχιστο χρονικό διάστημα, οι δύο δίσκοι θα απομακρυνθούν κινούμενοι όπως στο σχήμα (β).

Όμως, στο πρόβλημά μας, υπάρχουν δύο ακλόνητοι άξονες περιστροφής κάθετοι στα κέντρα των δύο δίσκων   και, όπως φαίνεται από την παραπάνω ανάλυση, αυτοί οι δύο άξονες δε θα επιτρέψουν τη μεταφορική κίνηση των δύο δίσκων. Πρέπει, λοιπόν, στη διάρκεια που οι δύο περιφέρειες ασκούν τριβή η μία στην άλλη, ο άξονας κάθε δίσκου να ασκεί δύναμη αντίθετη της τριβής που δέχεται, (στο σχήμα γ φαίνονται με μπλε χρώμα), ώστε να ισχύει σε καθένα δίσκο η συνθήκη ΣF = 0*. 

Οι δυνάμεις αυτές των αξόνων είναι εξωτερικές δυνάμεις, και για το σύστημα των δύο δίσκων αποτελούν ζεύγος εξωτερικών δυνάμεων. Αν γνωρίζουμε τις τριβές Τ, τότε στο σύστημα των δύο δίσκων ενεργεί μια εξωτερική ροπή -Τ(r₁ + r₂) κατά τη φορά των δεικτών του ρολογιού (αρνητική).

Επειδή η εξωτερική ροπή έχει φορά αντίθετη από την αρχική στροφορμή του συστήματος, η στροφορμή του συστήματος μειώνεται.

* Ουσιαστικά, η ροπή Tr₁ ή Tr₂, σε κάθε δίσκο, είναι η ροπή του ζεύγους των δυνάμεων Τ που ενεργεί σε καθένα από αυτούς.

Στο σύστημα των δύο δίσκων ενεργούν, επίσης, και άλλα δύο ζεύγη δυνάμεων με μηδενική ροπή, αφού οι άξονές τους ταυτίζονται. Είναι οι οριζόντιες δυνάμεις Ν με τις οποίες οι άξονες κρατούν σε επαφή τους δύο δίσκους (οι κόκκινες, που είναι εσωτερικές στο σύστημα των δύο δίσκων, απαραίτητες για την εμφάνιση των τριβών, Τ = μΝ) και οι μπλε που είναι εξωτερικές δυνάμεις από τους δύο άξονες προς τους δίσκους, με συνισταμένη μηδέν.  

Είναι, λοιπόν, φανερό ότι δεν μπορούμε να εφαρμόσουμε καμία από τις αρχές διατήρησης (ενέργειας ή στροφορμής).

Τότε, πώς θα λύσουμε την άσκηση;

Μόνο με τη βοήθεια του θεμελιώδη νόμου της στροφικής κίνησης:

Έστω Δt το χρονικό διάστημα ολίσθησης των περιφερειών των δύο δίσκων. Όταν οι περιφέρειες σταματήσουν να ολισθαίνουν μεταξύ τους, τότε τα σημεία επαφής τους θα έχουν ίσες ταχύτητες (υ₁ = υ₂  → ω₁r₁ = ω₂r₂) και έτσι θα σταματήσουν να τρίβονται μεταξύ τους (Τ = 0).

Για κάθε δίσκο ο θεμελιώδης νόμος της στροφικής κίνησης (Στ = ΔL/Δt) παίρνει τη μορφή:

                                 -Τr₁ = I₁(ω₁ – ω₀)/Δt,   για τον δίσκο 1, και

                                  Τr₂ = I₂(ω₂ – 0)/Δt,     για το δίσκο 2

Διαιρούμε:                 

                                  - r₁/r₂ = [I₁(ω₁ – ω₀)]/I₂ω₂

Από την ισότητα των ταχυτήτων προκύπτει ότι ω₂ = ω₁r₁/r₂ και αν θέσουμε αυτή την τιμή του ω₂ στην παραπάνω σχέση, θα βρούμε τελικά:

                                      ω₁ = (Ι₁ω₀)/[Ι₁ + (r₁/r₂)²I₂]

Το παράδοξο της συνολικής στροφορμής δύο δίσκων

 Ένας μαθητής, μου έστειλε το παρακάτω πρόβλημα που τους έδωσε ο καθηγητής τους:

«Οι δύο οριζόντιοι κυκλικοί δίσκοι 1 και 2 μπορούν να περιστρέφονται, ο καθένας, γύρω από ακλόνητο κατακόρυφο άξονα κάθετο στην επιφάνειά τους, που διέρχεται από το κέντρο τους, χωρίς τριβές. Οι ροπές αδράνειάς τους ως προς τον άξονα περιστροφής τους είναι Ι₁ και Ι₂, αντίστοιχα, και οι ακτίνες τους r₁ και r₂ .

Αρχικά ο δίσκος 1 περιστρέφεται με σταθερή γωνιακή ταχύτητα ω₀ , ενώ ο 2 είναι ακίνητος. Χωρίς να αλλάξουμε τον προσανατολισμό των αξόνων τους, πλησιάζουμε τους δύο δίσκους και τους φέρνουμε σε επαφή. Οι περιφέρειες των δύο δίσκων  γλιστρούν αρχικά η μια ως προς την άλλη, αλλά τελικά η ολίσθηση αυτή σταματά, λόγω της μεταξύ τους τριβής. Να βρείτε την τελική γωνιακή ταχύτητα ω₁ του δίσκου 1 ».  

Μου γράφει: « Σκέφτηκα πως δεν μπορώ να πάρω Α.Δ.Μ.Ε για το σύστημα, γιατί οι τριβές μεταξύ των δύο δίσκων θα μετατρέψουν μέρος της κινητικής ενέργειας του δίσκου 1 σε θερμότητα.

Γνωρίζω όμως ότι, εάν η συνολική εξωτερική ροπή σε ένα σύστημα είναι μηδέν, η ολική στροφορμή του συστήματος παραμένει σταθερή. Εδώ, το σύστημα των δύο δίσκων είναι μονωμένο. Οι εξωτερικές δυνάμεις είναι τα βάρη των δύο δίσκων και οι δυνάμεις από τα στηρίγματα των αξόνων περιστροφής. Αυτές όμως εξουδετερώνονται αφού το σύστημα δεν μετατοπίζεται κατακόρυφα, άρα εξουδετερώνονται και οι ροπές τους. Οι δυνάμεις των τριβών ανάμεσα στις περιφέρειες των δύο δίσκων είναι εσωτερικές δυνάμεις και η ολική ροπή των εσωτερικών δυνάμεων είναι μηδενική, αφού αυτές απαντούν κατά ζεύγη και έτσι έχουν αντίθετες ροπές. Αποφάσισα λοιπόν να εφαρμόσω Α.Δ.Σ:

                                                          Ι₁ω₀ = Ι₁ω₁ – Ι₂ω₂     (1)

Το (-) γιατί ο δίσκος 2 θα στραφεί δεξιόστροφα. Όταν παύουν να ολισθαίνουν μεταξύ τους, τα σημεία των περιφερειών των δύο δίσκων έχουν ίδια ταχύτητα, δηλ. 

                                           υ₁ = υ₂  ή ω₁r₁ = ω₂r₂  →  ω_{2 =} ω₁r_1/ r₂ , 

οπότε από την (1) έχουμε τελικά:

                                                        ω₁ = Ι₁ω₀/(Ι₁  – Ι₂r₁/r₂)

Όμως ο καθηγητής μου, λέει ότι η λύση αυτή είναι λάθος γιατί το σύστημα δεν είναι μονωμένο  καθώς υπάρχει μια εξωτερική ροπή που ενεργεί πάνω του. Δεν καταλαβαίνω ποια είναι η εξωτερική ροπή στη συγκεκριμένη περίπτωση.

Μπορείτε να μου εξηγήσετε σας παρακαλώ;

Κούνια και διατήρηση στροφορμής, η ερώτηση

Το κέντρο μάζας του παιδιού, με λυγισμένα τα γόνατα, βρίσκεται σε απόσταση ΟΒ από τον άξονα περιστροφής της κούνιας, ο οποίος διέρχεται από το σημείο Ο. Η κούνια μαζί με το παιδί αφήνονται από την ηρεμία (θέση 1), και όταν το κέντρο μάζας φτάσει στο χαμηλότερο σημείο Α της τροχιάς του (θέση 3) το παιδί σηκώνεται ξαφνικά όρθιο, ανεβάζοντας έτσι το κέντρο μάζας του από τη θέση Α στην θέση Α΄.

Να επιλέξετε το σωστό σε καθεμιά από τις παρακάτω προτάσεις και να αιτιολογήσετε την επιλογή σας.

Ι. Το μέτρο της στροφορμής του παιδιού, γύρω από το Ο, κατά την άνοδο του κέντρου μάζας του από το Α στο Α΄,

Κούνια και διατήρηση στροφορμής, η άσκηση

                              

Έστω ότι το κέντρο μάζας (σημείο B) ενός παιδιού, που κάθεται πατώντας με λυγισμένα τα γόνατα σε μια ελαφριά κούνια, βρίσκεται σε ύψος 1,2 m πάνω από το έδαφος. Το βάρος του παιδιού είναι 400 Ν και το κέντρο μάζας του, με λυγισμένα τα γόνατα, απέχει 3,7 m από τον άξονα περιστροφής της κούνιας, ο οποίος διέρχεται από το σημείο Ο. Η κούνια μαζί με το παιδί αφήνονται από την ηρεμία, και όταν το κέντρο μάζας φτάσει στο χαμηλότερο σημείο Α της τροχιάς του το παιδί σηκώνεται ξαφνικά όρθιο, ανεβάζοντας έτσι το κέντρο μάζας του από τη θέση Α στην θέση Α΄, κατά 0,6 m ψηλότερα. Να βρείτε:

Ένα παιδικό παιχνίδι με μάλλον απρόσμενη συμπεριφορά. ( Η άσκηση)

 Ένα παιδικό παιχνίδι αποτελείται από την τραπεζοειδή σφήνα του σχήματος, η οποία περιστρέφεται γύρω από τον σταθερό κατακόρυφο άξονα zz΄.

Το κυλινδρικό σώμα Σ, μάζας m = 0,18 kg, φέρει οπή κατά μήκος  του άξονά του και μπορεί να ολισθαίνει χωρίς τριβές πάνω στη λεπτή ράβδο ΑΒ.

Όταν η σφήνα περιστρέφεται με σταθερή γωνιακή ταχύτητα ω, το σώμα ισορροπεί σε απόσταση ℓ = 3/8 m από το Β.

Ένα παιδικό παιχνίδι με μάλλον απρόσμενη συμπεριφορά. (Η ερώτηση)

Ένα παιδικό παιχνίδι αποτελείται από την τραπεζοειδή σφήνα του σχήματος, η οποία περιστρέφεται γύρω από τον σταθερό κατακόρυφο άξονα zz΄.

Το κυλινδρικό σώμα Σ, μάζας m = 0,18 kg, φέρει οπή κατά μήκος  του άξονά του και μπορεί να ολισθαίνει χωρίς τριβές πάνω στη λεπτή ράβδο ΑΒ.

Όταν η σφήνα περιστρέφεται με σταθερή γωνιακή ταχύτητα ω, το σώμα ισορροπεί σε απόσταση ℓ από το Β και η στροφορμή του ως προς τον άξονα zz΄ έχει τιμή L.

Αν το σύστημα στρέφεται με γωνιακή ταχύτητα μέτρου ω΄= 2ω, τότε το σώμα ισορροπεί σε μια θέση όπου:

Όπου οι τριβές είναι στο όριό τους

Δύο παρόμοιοι ξύλινοι κύβοι, βάρους w = 15 N, υποστηρίζονται από μια αβαρή ράβδο με κλίση 45^ο ως προς το οριζόντιο επίπεδο, όπως φαίνεται στο σχήμα. Αν και οι δύο κύβοι βρίσκονται σε κατάσταση οριακής ισορροπίας* και ο συντελεστής οριακής στατικής τριβής (μ_w) μεταξύ του κύβου Β και το τοίχου είναι 0,5, τότε:

“Υγρή” ταλάντωση

Ο ανοικτός και στις δύο βάσεις  του κατακόρυφος κυλινδρικός σωλήνας του σχήματος, σταθερής διατομής Α, συγκρατείται ημιβυθισμένος σε μια δεξαμενή μεγάλης επιφάνειας γεμάτη με νερό. Αρχικά το σύστημα “σώμα Σ – έμβολο” ισορροπεί όπως στο σχήμα (α).

Αφήνουμε ελεύθερο το σώμα Σ, το έμβολο ανέρχεται και νερό εισχωρεί στον σωλήνα.

Αν δεν υπάρχουν απώλειες λόγω τριβών και αν η μάζα του εμβόλου είναι αμελητέα, να δείξετε ότι:

α. Υπάρχει θέση, όπου η ταχύτητα του σώματος Σ γίνεται μέγιστη και να βρείτε την απόστασή της από την αρχική του θέση.

Αναρρόφηση νερού σε μέγιστο ύψος με τη βοήθεια εμβόλου

Αναφερόμαστε στην  προηγούμενη άσκηση, με τη διαφορά ότι τώρα το κάτω ανοικτό άκρο του κατακόρυφου σωλήνα συγκρατείται ημιβυθισμένο σε μια δεξαμενή μεγάλης επιφάνειας, γεμάτη με νερό. Αρχικά το σύστημα “σώμα Σ – έμβολο” ισορροπεί όπως στο σχήμα (α).

Αφήνουμε ελεύθερο το σώμα Σ, το έμβολο ανέρχεται και νερό εισχωρεί στον σωλήνα.

Αν δεν υπάρχουν απώλειες λόγω τριβών και αν η μάζα του εμβόλου είναι αμελητέα σε σχέση με τη μάζα m του σώματος Σ, τότε το μέγιστο ύψος στο οποίο θα φτάσει το νερό στο σωλήνα, μετρούμενο από την επιφάνεια

Άντληση νερού και ισορροπία

Το έμβολο του σχήματος εφαρμόζει αεροστεγώς στα εσωτερικά τοιχώματα ενός κατακόρυφου κυλινδρικού σωλήνα, που είναι ανοικτός και στα δύο του άκρα και μπορεί να κινείται μέσα σε αυτόν χωρίς τριβές. Στην αρχή ισορροπεί στη θέση που φαίνεται στο σχήμα (α), με τη βοήθεια ενός σχοινιού στην άλλη άκρη του οποίου έχουμε κρεμάσει ένα σώμα Σ μάζας m. Αρχικά συγκρατούμε το σώμα για να μην κινηθεί προς τα κάτω. Ο σωλήνας είναι ημιβυθισμένος μέσα σε ένα δοχείο που περιέχει νερό όγκου 2L. Αφήνουμε σιγά – σιγά το σώμα Σ να κατέβει, με αποτέλεσμα το έμβολο να ανέβει και να εισέλθει νερό μέσα στο σωλήνα.

Σταθεροποίηση στάθμης και βεληνεκούς με δύο τρόπους. Ένα ακόμη θέμα Β στα ρευστά

Το κυλινδρικό δοχείο του σχήματος περιέχει νερό, του οποίου η ελεύθερη επιφάνεια φτάνει σε ύψος  Η₀ από τη βάση του.  Ανοίγουμε μια τρύπα εμβαδού α m² σε ύψος h < H₀/2 και το νερό αρχίζει να εκτινάσσεται από αυτήν με αρχική οριζόντια ταχύτητα πέφτοντας τελικά στο έδαφος. Ταυτόχρονα, ανοίγουμε μια βρύση και αρχίζουμε να παρέχουμε νερό στο δοχείο με σταθερή παροχή Π_β = α√2gh  m³/s.
 Ι. Η  στάθμη του νερού στο δοχείο:

α. Παραμένει στο ύψος Η₀.

β. Αρχίζει να πέφτει και κάποια στιγμή σταθεροποιείται σε ύψος 2h.

γ. Αρχίζει να πέφτει και κάποια στιγμή σταθεροποιείται στο ύψος h.

ΙΙ. Το βεληνεκές της φλέβας:

Τρία πρωτότυπα θέματα Β στα ρευστά 1. Η κούπα του Πυθαγόρα

Στο σχήμα (α) έχουμε σχεδιάσει την «κούπα του Πυθαγόρα», όπου μέσω ενός ανοίγματος, το υγρό που προσθέτουμε, εκτός από τον εμφανή χώρο στο εσωτερικό του κυπέλλου, εισχωρεί και στο κατακόρυφο “κρυφό” κανάλι ΔΕ (σχήμα β), το οποίο επικοινωνεί με δεύτερο ανοικτό κατακόρυφο κανάλι ΕΖ σταθερής διατομής. Αυτό διατρέχει τον κορμό του κύπελου και καταλήγει σε ένα άνοιγμα (στο σημείο Ζ) της βάσης του. Έτσι, αν η στάθμη του υγρού είναι χαμηλότερα από το σημείο Ε, δηλαδή ως το ύψος h (σχήματα β, γ), αυτό παραμένει μέσα στο κύπελλο, αν όμως ξεπεράσει το σημείο Ε τότε το υγρό οδηγείται στο κανάλι ΕΖ και από εκεί βγαίνει έξω από το κύπελλο, από το άνοιγμα της βάσης του στο σημείο Ζ.

 
Στο σχήμα (δ), ένα ιδανικό υγρό πυκνότητας ρ ισορροπεί μέσα σε ένα τέτοιο κύπελλο με τη στάθμη του σε ύψος Η > h, δεν χύνεται όμως γιατί  έχουμε σφηνώσει ένα κομμάτι φελλού στο άνοιγμα της βάσης του κύπελου.  Στη συνέχεια αφαιρούμε το φελλό και το υγρό αρχίζει να ρέει στο κανάλι ΔΕΖ και να εξέρχεται από το Ζ.

Τι από τα παρακάτω θα συμβεί:

2. Δύο πίδακες που εκτινάσσονται οριζόντια από δύο διαφορετικά βάθη h1 και h2 συναντιούνται σε βάθος h1+h2

Δύο πίδακες που εκτινάσσονται οριζόντια από δύο διαφορετικά βάθη h₁ και h₂ συναντιούνται. Στην άσκηση αυτή θα δούμε τι αντιπροσωπεύουν οι παραστάσεις: 

	_______
h1 + h2  και  2 √	h1h2

Άσκηση:

Το ανοικτό δοχείο του σχήματος περιέχει νερό. Σε δύο σημεία E και Z της ίδιας κατακορύφου του τοιχώματος του δοχείου και σε βάθη h₁ και h₂, αντίστοιχα, ανοίγουμε δύο οπές πολύ μικρής διατομής από τις οποίες εκτοξεύονται δύο πίδακες νερού.

Ι. Η απόσταση y_Σ, του σημείου συνάντησης Σ των δύο πιδάκων από την επιφάνεια του νερού, είναι ίση με:

	_______
α. 2(h1 - h2),       β.  h1 + h2        γ. 2√	h1h2