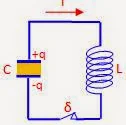
1. Σε ένα ιδανικό κύκλωμα LC ο πυκνωτής είναι μεταβλητής
χωρητικότητας και το πηνίο φέρει
σιδερένιο πυρήνα. Καθώς το κύκλωμα
εκτελεί ηλεκτρικές ταλαντώσεις, κάποια στιγμή, που το φορτίο του πυκνωτή είναι
μέγιστο, μεταβάλλουμε συγχρόνως και ακαριαία τη χωρητικότητα του πυκνωτή σε
τιμή διπλάσια της αρχικής και με
μετατόπιση του πυρήνα μειώνουμε το συντελεστή αυτεπαγωγής στο μισό. Τότε:
α. Η περίοδος του κυκλώματος ……………..
β. Η ενέργεια του κυκλώματος
………………..
γ. Το πλάτος της έντασης του
ρεύματος ……………………..
δ. Το πλάτος του φορτίου του πυκνωτή
…………………………..
2. Σε ιδανικό κύκλωμα ηλεκτρικών ταλαντώσεων να
δείξετε ότι μεταξύ της τάσης vC του πυκνωτή και της
έντασης i του
ρεύματος ισχύει η σχέση:
Όπου V και I οι μέγιστες τιμές,
αντίστοιχα, της τάσης του πυκνωτή και της έντασης του ρεύματος.
3. Σε ένα ιδανικό κύκλωμα LC που εκτελεί αρμονική ταλάντωση και
κάποια στιγμή το φορτίο του πυκνωτή είναι ίσο με το 60% της μέγιστης τιμή του,
η ένταση του ηλεκτρικού ρεύματος είναι ίση με:
α. Το 64% της μέγιστης τιμής της
β.
Το 36% της μέγιστης τιμής της
γ. Το 20% της μέγιστης τιμής της
δ. Το 80% της μέγιστης τιμής της
4. Το χρονικό
διάστημα στη διάρκεια μιας περιόδου που το φορτίο του ενός οπλισμού του πυκνωτή
σε ένα κύκλωμα LC είναι
μεγαλύτερο από +Q/2
είναι:
α. Τ/4, β.
Τ/3, γ. Τ/2, δ.
2Τ/3