Ηλεκτρομαγνητική επαγωγή και ισορροπία σε διαφορετικά επίπεδα

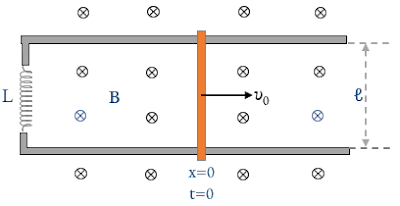
Δύο οριζόντιες αγώγιμες ράβδοι ΑΒ και ΓΔ ίδιας μάζας m και ίδιας αντίστασης R, μπορούν να ολισθαίνουν χωρίς τριβές πάνω σε δύο παράλληλους, μεγάλου μήκους  και αμελητέας αντίστασης, οδηγούς αγωγούς, οι οποίοι απέχουν μεταξύ τους οριζόντια απόσταση ℓ και αποτελούνται από οριζόντιο και πλάγιο τμήμα κλίσης φ ως προς το οριζόντιο επίπεδο. Το σύστημα των τεσσάρων αγωγών, όπως φαίνεται στο σχήμα, βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β με φορά προς τα κάτω.

Συγκρατούμε τη ράβδο ΑΒ και μέσω μιας κατάλληλης οριζόντιας δύναμης F, που εφαρμόζεται στο μέσον της ράβδου ΓΔ, παράλληλη προς τα οριζόντια τμήματα των οδηγών αγωγών, προσδίδουμε σταθερή ταχύτητα υ στη ράβδο ΓΔ.

α. Πόση πρέπει να είναι η ταχύτητα υ ώστε αν αφήσουμε τη ράβδο ΑΒ αυτή να παραμείνει ακίνητη; (τα μεγέθη m, g, ℓ,B, R και φ θεωρούνται γνωστά).

β. Πόση είναι τότε η δύναμη F με την οποία κινούμε τη ράβδο ΓΔ; 

Η λύση με κλικ εδώ

Δύο ράβδοι σε μαγνητικό πεδίο αλληλεπιδρούν (1ο)

 

Δύο παράλληλες αγώγιμες ακλόνητες ράγες μεγάλου μήκους και αμελητέας αντίστασης χωρίζονται με απόσταση ℓ.  Δύο πανομοιότυπες αγώγιμες ράβδοι τοποθετούνται στις ράγες κάθετα σε αυτές. Το όλο σύστημα βρίσκεται σε οριζόντιο επίπεδο. Κάθε ράβδος έχει μάζα M και ωμική αντίσταση R. Υπάρχει παντού ένα ομογενές μαγνητικό πεδίο που κατευθύνεται κάθετα προς στο επίπεδο της όλης διάταξης. Στη μία από τις δύο ράβδους δίνεται αρχική ταχύτητα υ₀ παράλληλη προς τις ράγες και με κατεύθυνση τέτοια ώστε να απομακρυνθεί αρχικά από την άλλη.

Απαντήστε στις ακόλουθες ερωτήσεις για το σύστημα των δύο ράβδων (αγνοείστε την τριβή και την αυτεπαγωγή):

α. Δείξτε ότι κάποτε οι δύο αγωγοί θα αποκτήσουν κοινή σταθερή ταχύτητα.

β. Θα μειωθεί η ορμή του συστήματος με το χρόνο;

γ. Ποια είναι η κινητική ενέργεια του συστήματος σε σταθερή κατάσταση;

Η λύση με κλικ εδώ

Πηνίο και κινούμενη ράβδος σε παράλληλες ράγες

 Μια αγώγιμη ράβδος μάζας m = 0,1 kg μπορεί να γλιστρήσει χωρίς τριβή πάνω σε δύο παράλληλες αγώγιμες ράγες που η μία απέχει από την άλλη απόσταση ℓ= 1 m. Οι αγώγιμες ράγες συνδέονται μέσω σωληνοειδούς αυτεπαγωγής L = 1 mH. Αυτό το σύστημα βρίσκεται σε οριζόντιο επίπεδο και τοποθετείται σε μια περιοχή που περιέχει ομογενές κατακόρυφο μαγνητικό πεδίο B = 1Τ με φορά προς τα κάτω.

Τη χρονική στιγμή t = 0 δίνουμε στη ράβδο αρχική ταχύτητα υ₀ = 1 m/s, προς τα δεξιά και την αφήνουμε ελεύθερη. Αν η συνολική ωμική αντίσταση στην όλη διάταξη είναι μηδέν, να δείξετε ότι η ράβδος θα εκτελέσει αρμονική ταλάντωση με πλάτος Α εκ. Να βρείτε:

α. Την τιμή του Α.

β. Τη μέγιστη ένταση του ρεύματος.

γ. Το μέγιστο ρυθμό μεταβολής του ρεύματος 

Η Λύση εδώ

Τι θα συμβεί στο ρεύμα κάθε πηνίου;

[Δύο πηνία με κοινό άξονα διαρρέονται από ρεύμα και πλησιάζουν ή απομακρύνονται μεταξύ τους. Τι θα συμβεί;]

Δύο παρόμοια ομοαξονικά πηνία διαρρέονται από ρεύματα ίδιας έντασης και φοράς. Τι θα συμβεί στο ρεύμα κάθε πηνίου αν πλησιάσουν το ένα προς το άλλο; 

Πτώση μαγνήτη μέσα από πηνίο

Ένας κυλινδρικός μαγνήτης αφήνεται ελεύθερος από κάποιο ύψος. Όπως φαίνεται στο σχήμα, ο βόρειος πόλος του μαγνήτη βρίσκεται στο κάτω άκρο του και ο νότιος πόλος στην κορυφή. Ο μαγνήτης κινείται προς τα κάτω κατά μήκος του κατακόρυφου άξονα ενός ακλόνητα στερεωμένου πηνίου. Τα άκρα του πηνίου  συνδέονται με ένα αμπερόμετρο. Υποθέστε ότι ο μαγνήτης ξεκινάει από μεγάλη απόσταση από το πηνίο, διέρχεται μέσα από αυτό και συνεχίζει την πτώση του μέχρι να απομακρυνθεί σε μεγάλη απόσταση από το πηνίο. Σε όλη τη διάρκεια της πτώσης του διατηρείται κατακόρυφα προσανατολισμένος, όπως ακριβώς τον αφήσαμε, με τον νότιο πόλο στην κορυφή του και τον βόρειο πόλο στο κάτω μέρος.

α) Αν θεωρήσουμε θετική την προς τα πάνω ροή των μαγνητικών γραμμών, και θετικό το ρεύμα στις σπείρες αν είναι αντίθετο προς τη φορά των δεικτών του ρολογιού, (όπως το βλέπουμε από πάνω), ποιο από τα παρακάτω γραφήματα, 

 αντιπροσωπεύει καλύτερα:

i. Τη γραφική παράσταση της μαγνητικής ροής μέσα από το πηνίο σε συνάρτηση με το χρόνο;

ii. Τη γραφική παράσταση της έντασης του ρεύματος στο πηνίο σε συνάρτηση με το χρόνο;

β) Υποθέστε ότι στη συνέχεια ανεβάζουμε με σταθερή ταχύτητα τον μαγνήτη, μετατοπίζοντάς τον πάνω στην ίδια, με αυτήν της πτώσης του, κατακόρυφο, από μια θέση πολύ πιο κάτω από το πηνίο ως μια θέση πολύ πιο πάνω από αυτό, χωρίς να του αλλάξουμε προσανατολισμό. Ποιο από τα προηγούμενα γραφήματα αντιπροσωπεύει καλύτερα:

i. Τη γραφική παράσταση της μαγνητικής ροής μέσα από το πηνίο σε συνάρτηση με το χρόνο;

ii. Τη γραφική παράσταση της έντασης του ρεύματος στο πηνίο σε συνάρτηση με το χρόνο;

γ) Αν διπλασιάσουμε τον αριθμό των σπειρών του πηνίου, χωρίς να αλλάξουμε την ταχύτητα, πώς θα αλλάξει το γράφημα της έντασης του ρεύματος με το χρόνο στην πιο πάνω περίπτωση;

Βλήμα διέρχεται μέσα από δύο παράλληλα μεταξύ τους πηνία

[Μια ευρεσιτεχνία από το 1949 για τη μέτρηση ταχύτητας βλήματος μέχρι 6 km/s]

Ένας μηχανισμός, βασισμένος στην επαγόμενη ΗΕΔ, έχει χρησιμοποιηθεί για να μετρήσει ταχύτητες βλήματος μέχρι 6 km /s. Ένας μικρός μαγνήτης είναι ενσωματωμένος στο βλήμα όπως φαίνεται στο σχήμα. Το βλήμα διέρχεται από δύο παράλληλα μεταξύ τους πηνία, που χωρίζονται από απόσταση d. Καθώς το βλήμα διέρχεται από κάθε πηνίο, προκαλείται εξ’ επαγωγής ένας παλμός ρεύματος. Το χρονικό διάστημα μεταξύ των παλμών αυτών μπορεί να μετρηθεί με ακρίβεια με ένα παλμογράφο και έτσι η ταχύτητα μπορεί να προσδιοριστεί.

α) Να δικαιολογήσετε την εμφάνιση των παλμών ρεύματος και να σχεδιάσετε σε κοινό διάγραμμα, με ελεύθερη εκτίμηση, την ένδειξη των αμπερομέτρων σε σχέση με το χρόνο t.  Θεωρείστε ένα ρεύμα που ρέει αριστερόστροφα, όπως φαίνεται από το σημείο εκκίνησης του βλήματος, ως θετικό. Στο γράφημά σας, υποδείξτε ποιος παλμός είναι από το πηνίο 1 και ποιος είναι από το πηνίο 2.

β) Εάν η χρονική διαφορά εμφάνισης των παλμών είναι Δt = 2 ms και η απόσταση των πηνίων είναι d = 2 m, να υπολογίσετε την ταχύτητα του βλήματος; 

Μαγνήτης κινούμενος επί του άξονα ενός κυκλικού πλαισίου 1ο.

[Πώς μεταβάλλονται η μαγνητική ροή και η ΗΕΔ από επαγωγή αν ένας μεγάλου μήκους μαγνήτης πλησιάζει με σταθερή ταχύτητα προς ένα κυκλικό βρόχο, διέρχεται και απομακρύνεται από αυτόν;]

 Ένας μακρύς κυλινδρικός μαγνήτης μήκους L και ακτίνας α φέρει στο εσωτερικό του ομογενές μαγνητικό πεδίο Β παράλληλο προς τον άξονά του. Πλησιάζει με σταθερή ταχύτητα υ, από σχετικά μεγάλη απόσταση, προς ένα κυκλικό αγώγιμο πλαίσιο ελαφρώς μεγαλύτερης διαμέτρου, κινούμενος διαρκώς κάθετα προς αυτό, με τον άξονά του να ταυτίζεται με τον άξονα του πλαισίου.  Διέρχεται μέσα από το πλαίσιο και συνεχίζει απομακρυνόμενος σε μεγάλη απόσταση.

α) Ποιο από τα πλαϊνά  διαγράμματα μπορεί να παριστάνει τη μεταβολή της μαγνητικής ροής με το χρόνο;

β) Να παραστήσετε γραφικά, με ελεύθερη εκτίμηση, την ΗΕΔ που επάγεται στο πλαίσιο σε συνάρτηση με το χρόνο. Θεωρείστε θετική τη μαγνητική ροή, η οποία οφείλεται στις δυναμικές γραμμές που διέρχονται μέσα από το πλαίσιο με φορά από δεξιά προς αριστερά. (Το διάνυσμα Α είναι το χαρακτηριστικό διάνυσμα της επιφάνειας του πλαισίου)

Παράλληλα πλαίσια. 2ο.

[Το ένα διαρρέεται από μεταβλητό ρεύμα. Αν αυξάνεται, έλκονται ή απωθούνται;]

Τα επίπεδα των δύο κυκλικών χάλκινων βρόχων του σχήματος είναι παράλληλα. Τα κέντρα τους βρίσκονται πάνω στον άξονα x΄x. Παρατηρώντας τους από αριστερά, ο βρόχος 1 διαρρέεται από αριστερόστροφο ρεύμα.

α) Εάν η ένταση του ρεύματος στον βρόχο 1 αυξάνεται, ποια είναι η κατεύθυνση του ρεύματος που προκαλείται στον βρόχο 2;

β) Οι βρόχοι έλκουν ή απωθούν ο ένας τον άλλον;

Εξηγήστε την απάντησή σας.

Τρία πλαίσια πάνω σε ένα ευθύγραμμο αγωγό

[Τι συμβαίνει όταν ο αγωγός διαρρέεται από συνεχές ρεύμα;]

Ένας μεγάλου μήκους ευθύγραμμος αγωγός, με μονωτικό περίβλημα, διαρρέεται από ρεύμα έντασης Ι. Πάνω στον αγωγό τοποθετούνται τρία ορθογώνια πλαίσια, με μήκος βάσης L και ύψος L, 1,5 L και 2L, αντίστοιχα, όπως φαίνεται στο σχήμα. Τα πλαίσια 1 και 2 τοποθετούνται συμμετρικά ως προς τον αγωγό. Να κατατάξετε τα πλαίσια σύμφωνα με την ένταση του επαγόμενου σε αυτά ρεύματος, αν το ρεύμα του ευθύγραμμου αγωγού (α) παραμένει σταθερό και (β) αυξάνεται.

Ξεκινήσετε πρώτα από το πλαίσιο στο οποίο επάγεται το μεγαλύτερης έντασης ρεύμα.

Να θεωρήσετε  ότι τα πλαίσια απέχουν αρκετά το ένα από το άλλο, ώστε να μην αλληλεπιδρούν μεταξύ τους.

Προσέγγιση και απομάκρυνση βρόχου από ρευματοφόρο αγωγό

 [Τι συμβαίνει όταν ένας συρμάτινος βρόχος κινείται προς έναν ευθύγραμμο ρευματοφόρο αγωγό και τι όταν απομακρύνεται από αυτόν;]

Ένας κυκλικός συρμάτινος βρόχος αφήνεται από κάποιο ύψος πάνω από έναν οριζόντιο ευθύγραμμο αγωγό, μεγάλου μήκους, που διαρρέεται από ρεύμα Ι με φορά από δεξιά προς τα αριστερά.

Ο βρόχος κινείται ευρισκόμενος διαρκώς σε κατακόρυφο επίπεδο παράλληλο προς τον αγωγό και σε οριακά μικρή απόσταση από αυτόν για να αποφευχθεί η σύγκρουση.

Ποια είναι η φορά του ρεύματος που επάγεται στο βρόχο, καθώς:

α. πλησιάζει προς τον ευθύγραμμο αγωγό,

β. απομακρύνεται από αυτόν;

Να αιτιολογήσετε την επιλογή σας. 

Ένα αγώγιμο πλαίσιο στην πόρτα

[Εμφανίζεται ηλεκτρικό ρεύμα σε ένα αγώγιμο πλαίσιο, ενσωματωμένο στο εσωτερικό μιας πόρτας, όταν την ανοιγοκλείνουμε;]

Το ορθογώνιο πλαίσιο της πόρτας έχει διαστάσεις h=1,5 m, ℓ=0,6 m και αντίσταση R=0,026 Ω.

Όταν η πόρτα είναι κλειστή (θ = 0 °), είναι κάθετη στην οριζόντια συνιστώσα του γήινου μαγνητικού πεδίου: B_Γ = 2,6 10^-5 T. Τη στιγμή t = 0 s ανοίγει η πόρτα και η δεξιά πλευρά της κινείται προς το εσωτερικό της σελίδας με σταθερή γωνιακή ταχύτητα ω = 0,5π r/s, ώστε η διαγραφόμενη γωνία θ να δίνεται από τη σχέση θ = ωt. Προσδιορίστε την κατεύθυνση και την ένταση του επαγόμενου ρεύματος τη χρονική στιγμή t = 1/3 s.

Δίνεται ότι, σε μικρή περιοχή, το μαγνητικό πεδίο της γης μπορεί να θεωρηθεί ομογενές. Στο σχήμα διακρίνεται η πρόσοψη και η κάτοψη της πόρτας, π = 3,14.

Απάντηση: 

Μαγνήτης κινούμενος κάθετα στον άξονα ενός κυκλικού βρόχου

[Τι συμβαίνει όταν ένας μαγνήτης κινείται προς ένα μεταλλικό κυκλικό βρόχο με τον άξονά του Ν-S παράλληλο προς το επίπεδο του βρόχου;]

Ένας ραβδόμορφος μαγνήτης σπρώχνεται προς ένα κυκλικό αγώγιμο βρόχο, όπως στο σχήμα. Σε όλη τη διάρκεια της κίνησή του, ο άξονάς του N-S διατηρείται παράλληλος  προς το επίπεδο του βρόχου και η κάθετος στο μέσον του μαγνήτη διέρχεται από το κέντρο του βρόχου.

Θα εμφανιστεί ρεύμα εξ’ επαγωγής στο δακτύλιο; Αν ναι, προς ποια κατεύθυνση; Αν όχι, γιατί;

 Απάντηση: 

Τρεις σιδερένιες ράγες σε ομογενές μαγνητικό και ένας κινούμενος αγωγός

(Ποιο Μήκος του κινούμενου αγωγού μετράει;)

Δίνεται η διάταξη που φαίνεται στο παραπάνω σχήμα. Ο ευθύγραμμος αγωγός ΑΓ έχει αμελητέα αντίσταση και μπορεί να ολισθαίνει πάνω σε τρείς ράγες με σταθερή ταχύτητα 10 cm/s. Βρείτε την ένταση του ρεύματος στην αντίσταση των 5 Ω όταν ο διακόπτης δ βρίσκεται:

α) Στη μεσαία ράγα

β) Στην κάτω ράγα.

Απάντηση: 

Ένα σύνθετο ομογενές μαγνητικό πεδίο. 1ο .

Πλαίσια σε περισσότερο από ένα ομογενή μαγνητικά πεδία

Το σχήμα δείχνει τρεις περιπτώσεις στις οποίες τρία ίδια ορθογώνια αγώγιμα πλαίσια είναι τοποθετημένα κάθετα μέσα σε ομογενή μαγνητικά πεδία, που είτε αυξάνουν (Α) είτε μειώνονται (Μ) σε μέγεθος με ίσους ρυθμούς. Σε κάθε μία, η διακεκομμένη γραμμή χωρίζει το πλαίσιο σε δύο ίσα τμήματα που βρίσκονται σε διαφορετικά μαγνητικά πεδία. Κατατάξτε τις τρεις αυτές περιπτώσεις σύμφωνα με το μέγεθος της έντασης του ρεύματος, που προκαλείται στον αντίστοιχο βρόχο, ξεκινώντας από τη μεγαλύτερη πρώτα.

Απάντηση: 

Ένα σύνθετο ομογενές μαγνητικό πεδίο. 2ο .

Περισσότερα από ένα μεταβαλλόμενα Ο.Μ.Π στο εσωτερικό ενός συρμάτινου πλαισίου. Πώς αντιμετωπίζουμε μια τέτοια περίπτωση;

Το σχήμα (1) δείχνει ένα σύρμα που σχηματίζει ένα ορθογώνιο με διαστάσεις ℓ = 0,3 m και w = 0,15 m και με ωμική αντίσταση R = 0,005 Ω. Το εσωτερικό του χωρίζεται σε τρεις ίσες περιοχές, με μαγνητικά πεδία Β₁, Β₂ και Β₃. Τα πεδία σε κάθε περιοχή είναι ομογενή κάθετα στην επιφάνεια του ορθογώνιου πλαίσιου με φορά τα Β₃ και Β₂ προς το εξωτερικό μέρος της σελίδας και το Β₁ προς το εσωτερικό. 

Το σχήμα (2) αποδίδει τη μεταβολή της έντασης κάθε πεδίου σε mT σε συνάρτηση με το χρόνο t.

Ποια είναι:

 (α) η ένταση 

(β) η φορά του ρεύματος που επάγεται στο σύρμα; 

Απάντηση:

Επαναδιατυπώνοντας και λύνοντας την άσκηση 55 του σχολικού βιβλίου με το νόμο του Faraday

Κινούμενη ράβδος σε πλαίσιο: Ο μαθητής προβληματίζεται ... 

" να εκφράσω τη μεταβολή της μαγνητικής ροής με το εμβαδόν που σαρώνει η ράβδος ή με τη μεταβολή του εμβαδού των δύο κελιών;" 

Γι’ αυτό, πιο κάτω προτείνεται μια επαναδιατύπωση της εκφώνησης της άσκησης 55 του σχολικού, που κατευθύνει και διευκολύνει τον μαθητή.

Μια αγώγιμη ράβδος με μηδενική αντίσταση και μήκος ℓ ολισθαίνει χωρίς τριβή με σταθερή ταχύτητα πάνω σε δύο παράλληλα, ευθύγραμμα, τέλεια αγώγιμα σύρματα. Οι αντιστάτες R₁ και R₂ συνδέονται κατά μήκος των άκρων των συρμάτων για να σχηματίσουν ένα κύκλωμα, όπως φαίνεται στο σχήμα. Ένα σταθερό μαγνητικό πεδίο Β κατευθύνεται κάθετα και προς το εσωτερικό της σελίδας. Για να υπολογίσετε τη μαγνητική ροή μέσω οποιασδήποτε επιφάνειας, πάρτε το κάθετο στην επιφάνεια χαρακτηριστικό διάνυσμά της να εισχωρεί στη σελίδα, παράλληλο με το Β.

α) Η μαγνητική ροή στον δεξιό βρόχο (Ι) του κυκλώματος:

 1) μειώνεται

2) αυξάνεται.

Ποιο είναι το μέγεθος του ρυθμού μεταβολής της μαγνητικής ροής στον δεξιό βρόχο;

β) Ποιο είναι το ρεύμα που ρέει μέσω του αντιστάτη R₂ στον δεξιό βρόχο του κυκλώματος; Υπολογίστε την έντασή  του και δείξτε την κατεύθυνση του στο σχήμα.

γ) Η μαγνητική ροή στον αριστερό βρόχο (ΙΙ) του κυκλώματος:

 1) μειώνεται

2) αυξάνεται.

Ποιο είναι το μέγεθος του ρυθμού μεταβολής της μαγνητικής ροής στον αριστερό βρόχο;

(δ) Ποιο είναι το ρεύμα που ρέει μέσω της αντίστασης R₂ στον αριστερό βρόχο του κυκλώματος; Βρείτε την ένταση του και δείξτε την κατεύθυνσή του στο σχήμα.

ε) Ποιο είναι το μέτρο και η κατεύθυνση της μαγνητικής δύναμης που ασκείται στη ράβδο;

Απάντηση σε pdf: 
Απάντηση σε word:

Επαγωγικό ρεύμα σε κυκλικό αγώγιμο βρόχο

"Το επαγωγικό ρεύμα σε κυκλικό αγώγιμο βρόχο, εντός ομαλά μεταβαλλόμενου Μ.Π., εξαρτάται μόνο από τη μάζα και από τη φύση του υλικού του"

Τα δύο χάλκινα δακτυλίδια στα σχήματα α και β, με διαφορετικές διαμέτρους D₁ και D₂ και διαφορετικές διατομές Α₁ και Α₂, έχουν ίδια μάζα m. Το καθένα βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο με την επιφάνειά του κάθετη προς τις δυναμικές του γραμμές. Αν η ένταση κάθε μαγνητικού πεδίου μεταβάλλεται με σταθερό ρυθμό έτσι ώστε dB₁/dt = dB₂/dt = λ, σε ποιο δακτυλίδι αναπτύσσεται μεγαλύτερο επαγωγικό ρεύμα;

Δίνεται ότι η ωμική αντίσταση ενός ομογενούς αγωγού σταθερής διατομής παρέχεται από τη σχέση R = ρℓ/Α, όπου ρ η ειδική αντίστασή του, ℓ το μήκος του και Α η διατομή του.

Αγώγιμος κυκλικός βρόχος πέφτει σε μαγνητικό πεδίο

Ένας αγώγιμος κυκλικός βρόχος, κατασκευασμένος από σύρμα αντίστασης R και μάζας m, πέφτει από μεγάλο ύψος μέσα σε ένα μαγνητικό πεδίο του οποίου οι δυναμικές γραμμές  παρουσιάζουν τη συμμετρία που βλέπετε στο σχήμα. Σε αυτό το μαγνητικό πεδίο, η κατακόρυφη συνιστώσα έχει σταθερή φορά προς τα πάνω και μεταβάλλεται σύμφωνα με τη σχέση B_z = B₀(1 + λz), όπου λ είναι κάποια σταθερά. Ο βρόχος, με εμβαδόν επιφάνειας S, σε όλη τη διάρκεια της πτώσης του παραμένει οριζόντιος, παράλληλος  προς το επίπεδο xy. 
Να δείξετε ότι ο βρόχος θα αποκτήσει οριακή ταχύτητα και να την υπολογίσετε.
Αγνοείστε την αντίσταση του αέρα και το μαγνητικό πεδίου του επαγόμενου ρεύματος. 
Δίνεται η επιτάχυνση της βαρύτητας g.  

Γιατί στο νόμο της επαγωγής του Faraday δεν λαμβάνουμε υπόψη και τη μαγνητική ροή του επαγόμενου ρεύματος;

Ερώτηση μαθητή: 

"Σε μια θέση που χαρακτηρίζεται από γωνία φ, η μαγνητική ροή στο πλαίσιο προέρχεται εν μέρει από το εξωτερικό πεδίο με σταθερή ένταση Β και εν μέρει από το μαγνητικό πεδίο του επαγόμενου ρεύματος. Γιατί στο νόμο της επαγωγής του Faraday δεν λαμβάνουμε υπόψη και τη μαγνητική ροή του επαγόμενου ρεύματος;"

Πλαίσιο στρεφόμενο γύρω από άξονα που τέμνει πλάγια τις δυναμικές γραμμές Ο.Μ.Π.

Οι δυναμικές γραμμές ενός ομογενούς μαγνητικού πεδίου σχηματίζουν γωνία φ = 60^ο με το οριζόντιο επίπεδο. Για τη μέτρηση της έντασης του πεδίου χρησιμοποιούμε ένα κυκλικό πλαίσιο, το οποίο συνδέεται με ευαίσθητο γαλβανόμετρο. Το πλαίσιο αποτελείται από Ν = 10 σπείρες που καθεμιά έχει εμβαδόν S = 5 cm². Η ολική αντίσταση του κυκλώματος είναι R = 4 Ω. Τοποθετούμε το πλαίσιο μέσα στο πεδίο, ώστε το επίπεδο των σπειρών του να είναι κατακόρυφο και παράλληλο προς τις δυναμικές γραμμές. Όταν το πλαίσιο στραφεί κατά γωνία θ = 90^ο γύρω από την κατακόρυφη διάμετρό του, το γαλβανόμετρο μετράει φορτίο Q = 200 μCb.

α. Να υπολογίσετε το μέτρο της έντασης του μαγνητικού πεδίου

β. Ποιο ηλεκτρικό φορτίο θα μετρήσει το γαλβανόμετρο, αν το πλαίσιο στραφεί κατά την ίδια γωνία θ = 90^ο γύρω από την οριζόντια διάμετρό του;

γ. Αν στρέφουμε το πλαίσιο γύρω από την κατακόρυφη διάμετρό του με σταθερή γωνιακή ταχύτητα ω = 60 r/s. Na υπολογίσετε το ποσό θερμότητας που ελευθερώνεται ανά λεπτό από την αντίσταση του συστήματος.

Να μη ληφθεί υπόψη το γήινο μαγνητικό πεδίο. 

Απάντηση: