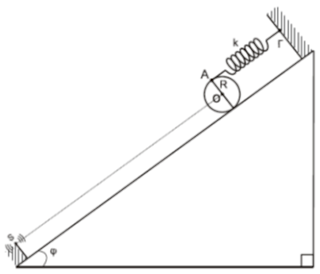
Μια σφαίρα Α ακτίνας R κινείται με ταχύτητα v και συγκρούεται ελαστικά με μια άλλη όμοια σφαίρα Β που αρχικά ηρεμεί. Το κέντρο της σφαίρας Β βρίσκεται σε απόσταση b από την ευθεία στην οποία κινείται το κέντρο της Α.
Στο χώρο αυτό, οι μαθητές της Γ Λυκείου αλλά και οι συνάδελφοι εκπαιδευτικοί θα βρουν μια σειρά από ερωτήσεις, πρωτότυπες ασκήσεις και προβλήματα στο πνεύμα των πανελλαδικών εξετάσεων. Το υλικό έχει ελεγχτεί και έχει πάρει την τελική του μορφή με τη συμβολή φίλων συνεργατών και ενός μεγάλου αριθμού μαθητών μου, μπορεί όμως ακόμη να έχει κάποιες ατέλειες. Οποιοδήποτε καλοπροαίρετο σχόλιο ή οποιαδήποτε διόρθωση είναι επιθυμητή.
Η φύση αγαπά την αλήθεια, και η αλήθεια της φύσης διεκδικεί το δικαίωμα να εκτίθεται μόνο σε όσους την ποθούν. Φ. Ντοστογιέφσκι
Σάββατο 29 Σεπτεμβρίου 2018
Ελαστική κρούση σε δυο διαστάσεις.
Μια σφαίρα Α ακτίνας R κινείται με ταχύτητα v και συγκρούεται ελαστικά με μια άλλη όμοια σφαίρα Β που αρχικά ηρεμεί. Το κέντρο της σφαίρας Β βρίσκεται σε απόσταση b από την ευθεία στην οποία κινείται το κέντρο της Α.
| _______ | |
| α. v√ | 1- (b/R)2 , β. vb⁄R , γ. vb⁄2R |
Απάντηση:
Τετάρτη 26 Σεπτεμβρίου 2018
Το πρότυπο του απλού αρμονικού ταλαντωτή
Απλή αρμονική ταλάντωση συστήματος "ιδανικού κατακόρυφου ελατηρίου - μάζας" σε πεδίο βαρύτητας
- Το πρώτο μέρος είναι αρκετά τυπικό και περιέχει βασικές γνώσεις α.α.τ.
- Το δεύτερο περιγράφει πώς δυο καλοί μαθητές μπορούν εύκολα να μπλέξουν "σαν τον Ηρακλή με τις κουβαρίστρες", ακριβώς επειδή είναι καλοί. Ευτυχώς που είναι δύο!
- Στο τρίτο μέρος οι συμμαθητές "γεννούν" μια ιδέα που ξεκαθαρίζει τη σχέση μεταξύ των τριών δυναμικών ενεργειών: βαρύτητας, ελαστικότητας και ταλάντωσης.
- Στο τέταρτο μέρος γίνεται αναλυτική παρουσίαση δύο σχετικών ασκήσεων.
- ΜΕΡΟΣ 1ο: Τα βασικά (μαζί με μια εφαρμογή)
- ΜΕΡΟΣ 2ο: Όπου δυο μαθητές, προσπαθούν να δώσουν απάντηση σε μια απλή αλλά ενδιαφέρουσα ερώτηση.
- ΜΕΡΟΣ 3ο: Όπου οι δυο μαθητές κάνουν μια "σημαντική ανακάλυψη" για τη Μηχανική ενέργεια ταλάντωσης συστήματος "κατακόρυφου ελατηρίου – μάζας".
- ΜΕΡΟΣ 4ο: Όλες οι δυναμικές ενέργειες μαζί. (Δύο ασκήσεις με τη λύση τους)
Παρασκευή 21 Σεπτεμβρίου 2018
Απλή Αρμονική Ταλάντωση. Δέκα ερωτήσεις
Τετάρτη 19 Σεπτεμβρίου 2018
8. Ελαστική κρούση τριών σωμάτων. Ολική μεταφορά.
 Τρεις τέλεια λείες ελαστικές σφαίρες Α, Β και Γ, με
μάζες mA = 2 kg, mB = 4kg και mΓ = 8 kg, κινούνται κατά
μήκος της ευθείας που ενώνει τα κέντρα τους και προς την ίδια κατεύθυνση με
ταχύτητες μέτρων 4 m/s, 1m/s και 0,75 m/s, αντίστοιχα, όπως δείχνει το σχήμα. Αν πρώτα
συγκρουστεί η σφαίρα Α με τη Β, και στη συνέχεια η Β με τη Γ, τότε:
Τρεις τέλεια λείες ελαστικές σφαίρες Α, Β και Γ, με
μάζες mA = 2 kg, mB = 4kg και mΓ = 8 kg, κινούνται κατά
μήκος της ευθείας που ενώνει τα κέντρα τους και προς την ίδια κατεύθυνση με
ταχύτητες μέτρων 4 m/s, 1m/s και 0,75 m/s, αντίστοιχα, όπως δείχνει το σχήμα. Αν πρώτα
συγκρουστεί η σφαίρα Α με τη Β, και στη συνέχεια η Β με τη Γ, τότε:Δευτέρα 17 Σεπτεμβρίου 2018
Ελαστική κρούση και ανατροπή
Τρίτη 11 Σεπτεμβρίου 2018
Ταχύτητα απομάκρυνσης προς ταχύτητα προσέγγισης
Δευτέρα 10 Σεπτεμβρίου 2018
Εισαγωγικές εξετάσεις 2018 τέκνων Ελλήνων Εξωτερικού στη Φυσική: Θέματα - Απαντήσεις
Παρασκευή 7 Σεπτεμβρίου 2018
Επαναληπτικές Πανελληνίων 2018 στη Φυσική : Θέματα - Απαντήσεις
9. Μια κεντρική κρούση όπου υ1,τελ ≤ υ1,αρχ/2
Πέμπτη 6 Σεπτεμβρίου 2018
Τρία τετράγωνα κι ένα στρογγυλό πλακάκι. Μια “περίεργη” κρούση
Τετάρτη 5 Σεπτεμβρίου 2018
Δύο σφαίρες σε λείο κυκλικό αυλάκι. Μια όμορφη συμμετρία
Δύο μικρές λείες ελαστικές σφαίρες Α και Β με μάζες
3m και m, αντίστοιχα, ηρεμούν αρχικά μέσα σε ένα οριζόντιο λείο
κυκλικό αυλάκι σε θέσεις αντιδιαμετρικές. Τη στιγμή t = 0 δίνουμε μια
ώθηση στη σφαίρα Α, η οποία αρχίζει να κυλά με σταθερή γραμμική ταχύτητα υ και
μετά από χρόνο t0 = 2 sec συγκρούεται για 1η φορά,
κεντρικά, με τη σφαίρα Β.
Να βρείτε:
α. Ποια χρονική στιγμή και σε ποια θέση οι δύο σφαίρες
θα συγκρουστούν για 2η φορά.
Δύο ελαστικές σφαίρες σε λείο κυκλικό αυλάκι – πότε θα ξανασυγκρουστούν.
Δύο μικρές λείες ελαστικές σφαίρες ηρεμούν, αρχικά,
μέσα σε ένα οριζόντιο λείο κυκλικό αυλάκι, σε θέσεις αντιδιαμετρικές. Δίνουμε
μια ώθηση στη σφαίρα Α, η οποία αρχίζει να κυλά με σταθερή γωνιακή ταχύτητα,
και μετά από χρόνο t0 συγκρούεται κεντρικά με τη σφαίρα Β.
Μετά την κρούση οι δύο σφαίρες θα ξανασυγκρουστούν έπειτα από χρόνο:
α. t0, αν mA > mB,
και 2t0, αν mA < mB
Δύο σφαίρες σε λείο κυκλικό αυλάκι και «το παράδοξο της 2ης κρούσης»
Δύο μικρές λείες ελαστικές σφαίρες τοποθετούνται σε
ένα οριζόντιο λείο κυκλικό αυλάκι, σε θέσεις αντιδιαμετρικές. Σπρώχνουμε τις
δύο σφαίρες να κινηθούν αντίθετα με ταχύτητες υΑ και
υΒ, αντίστοιχα. Οι δύο σφαίρες κινούνται με σταθερή γωνιακή ταχύτητα
και μετά από χρόνο t0 συγκρούονται
κεντρικά.
α. Σε πόσο χρόνο οι δύο σφαίρες θα ξανασυγκρουστούν;