[Μια απλή άσκηση συνδυασμού στροφικής κίνησης τριών σωμάτων, που
μπορεί να διαμορφωθεί σε ΘΕΜΑ Β]
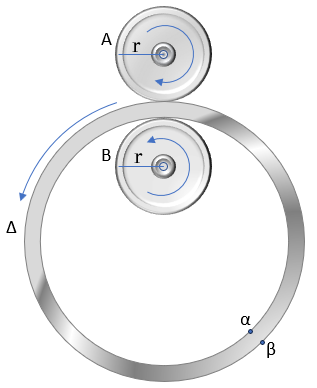
Το σύστημα σωμάτων του σχήματος αποτελείται
από δύο όμοιους ομογενείς κατακόρυφους τροχούς Α, Β και έναν ομογενή δακτύλιο
Δ. Οι τροχοί Α και Β ακτίνας r = 4 cm μπορούν να περιστρέφονται γύρω από
ακλόνητους οριζόντιους άξονες κάθετους στο κέντρο τους. Ο δακτύλιος Δ, με
εσωτερική ακτίνα Rεσ = 11 cm και εξωτερική ακτίνα Rεξ = 12 cm, είναι τοποθετημένος ανάμεσα στους δύο
τροχούς. Γνωρίζοντας ότι ο τροχός Α περιστρέφεται κατά τη φορά των δεικτών του
ρολογιού, με τη βοήθεια ενός κινητήρα κατάλληλα προσαρμοσμένου στον άξονά του,
με σταθερή συχνότητα fA = 3 c/s και
ότι δεν λαμβάνει χώρα ολίσθηση να βρείτε:
α. Τη γωνιακή ταχύτητα του τροχού Β.
β. Την επιτάχυνση των σημείων των τροχών Α
και Β τα οποία είναι σε επαφή με τον δακτύλιο.
γ. Το λόγο των στροφορμών των υλικών
σημείων α και β, εσωτερικού και εξωτερικού, αντίστοιχα, του δακτυλίου.
Θεωρείστε ότι Δmα = Δmβ και π2 ≈ 10.
Η απάντηση με κλικ εδώ.