Σταθεροποίηση στάθμης και βεληνεκούς με δύο τρόπους. Ένα ακόμη θέμα Β στα ρευστά

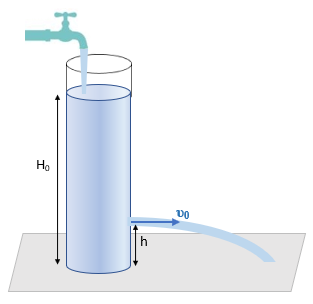
Το κυλινδρικό δοχείο του σχήματος περιέχει νερό, του οποίου η ελεύθερη επιφάνεια φτάνει σε ύψος  Η₀ από τη βάση του.  Ανοίγουμε μια τρύπα εμβαδού α m² σε ύψος h < H₀/2 και το νερό αρχίζει να εκτινάσσεται από αυτήν με αρχική οριζόντια ταχύτητα πέφτοντας τελικά στο έδαφος. Ταυτόχρονα, ανοίγουμε μια βρύση και αρχίζουμε να παρέχουμε νερό στο δοχείο με σταθερή παροχή Π_β = α√2gh  m³/s.
 Ι. Η  στάθμη του νερού στο δοχείο:

α. Παραμένει στο ύψος Η₀.

β. Αρχίζει να πέφτει και κάποια στιγμή σταθεροποιείται σε ύψος 2h.

γ. Αρχίζει να πέφτει και κάποια στιγμή σταθεροποιείται στο ύψος h.

ΙΙ. Το βεληνεκές της φλέβας:

Τρία πρωτότυπα θέματα Β στα ρευστά 1. Η κούπα του Πυθαγόρα

Η ΚΟΥΠΑ ΤΟΥ ΠΥΘΑΓΟΡΑ

Στο σχήμα (α) έχουμε σχεδιάσει την «κούπα του Πυθαγόρα», όπου μέσω ενός ανοίγματος, το υγρό που προσθέτουμε, εκτός από τον εμφανή χώρο στο εσωτερικό του κυπέλλου, εισχωρεί και στο κατακόρυφο “κρυφό” κανάλι ΔΕ (σχήμα β), το οποίο επικοινωνεί με δεύτερο ανοικτό κατακόρυφο κανάλι ΕΖ σταθερής διατομής. Αυτό διατρέχει τον κορμό του κύπελου και καταλήγει σε ένα άνοιγμα (στο σημείο Ζ) της βάσης του. Έτσι, αν η στάθμη του υγρού είναι χαμηλότερα από το σημείο Ε, δηλαδή ως το ύψος h (σχήματα β, γ), αυτό παραμένει μέσα στο κύπελλο, αν όμως ξεπεράσει το σημείο Ε τότε το υγρό οδηγείται στο κανάλι ΕΖ και από εκεί βγαίνει έξω από το κύπελλο, από το άνοιγμα της βάσης του στο σημείο Ζ.

 

 Στο σχήμα (δ), ένα ιδανικό υγρό πυκνότητας ρ ισορροπεί μέσα σε ένα τέτοιο κύπελλο με τη στάθμη του σε ύψος Η > h, δεν χύνεται όμως γιατί  έχουμε σφηνώσει ένα κομμάτι φελλού στο άνοιγμα της βάσης του κύπελου.  Στη συνέχεια αφαιρούμε το φελλό και το υγρό αρχίζει να ρέει στο κανάλι ΔΕΖ και να εξέρχεται από το Ζ.

Τι από τα παρακάτω θα συμβεί:

2. Δύο πίδακες που εκτινάσσονται οριζόντια από δύο διαφορετικά βάθη h1 και h2 συναντιούνται σε βάθος h1+h2

Δύο πίδακες που εκτινάσσονται οριζόντια από δύο διαφορετικά βάθη h₁ και h₂ συναντιούνται. Στην άσκηση αυτή θα δούμε τι αντιπροσωπεύουν οι παραστάσεις: 

	_______
h1 + h2  και  2 √	h1h2

Άσκηση:

Το ανοικτό δοχείο του σχήματος περιέχει νερό. Σε δύο σημεία E και Z της ίδιας κατακορύφου του τοιχώματος του δοχείου και σε βάθη h₁ και h₂, αντίστοιχα, ανοίγουμε δύο οπές πολύ μικρής διατομής από τις οποίες εκτοξεύονται δύο πίδακες νερού.

Ι. Η απόσταση y_Σ, του σημείου συνάντησης Σ των δύο πιδάκων από την επιφάνεια του νερού, είναι ίση με:

	_______
α. 2(h1 - h2),       β.  h1 + h2        γ. 2√	h1h2

3. Με πόση δύναμη συγκρατούσε ο Torricelli τον κατακόρυφο σωλήνα;

Όταν άκουσε η Σοφία την εξήγηση στο γιατί ο Torricelli, στο ομώνυμο πείραμά του, συγκρατούσε το σωλήνα έτσι ώστε να μην ακουμπάει στον πυθμένα του δοχείου, αναρωτήθηκε αυθόρμητα: 
- Με πόση άραγε δύναμη; 
Στερεώσαμε το σωλήνα σε ένα ελατήριο... 
- Φυσικά, με δύναμη ίση με αυτήν που ασκεί το ελατήριο στο σωλήνα με τον υδράργυρο!! 
Αποφάνθηκε ο Γιάννης 🌝...

Οι δύο αντεστραμμένοι κατακόρυφοι γυάλινοι σωλήνες, κλειστοί στο πάνω άκρο τους και αμελητέου βάρους, περιέχουν ο πρώτος νερό (με το οποίο είναι γεμάτος), και ο δεύτερος υδράργυρο ως ένα ύψος (από εκεί και πάνω υπάρχει κενό). Το ανοικτό στόμιο του πρώτου είναι βυθισμένο μέσα σε νερό, ενώ του δεύτερου σε υδράργυρο.

Ι. Για καθεμιά περίπτωση χωριστά, τι από τα παρακάτω είναι σωστό:

α. Δύναμη ελατηρίου > βάρος υγρού στο σωλήνα*

Μια αντλία προωθεί Νευτώνειο ρευστό σε οριζόντιο σωλήνα

Στην έξοδο μιας αντλίας νερού συνδέεται ένας οριζόντιος σωλήνας σταθερής διατομής Α = 20 cm². Στην αρχή του σωλήνα αυτού, η αντλία εισάγει το νερό που απορροφά από μια υπόγεια δεξαμενή και το προωθεί υπό πίεση Ρ_εισ = 400 kPa.

Το άλλο άκρο του σωλήνα είναι ανοικτό στην ατμόσφαιρα, όπου επικρατεί πίεση ίση με 100 kPa.

Το νερό συμπεριφέρεται ως Νευτώνειο υγρό, οπότε η αντλία καταναλώνει ισχύ ώστε αυτό να κινείται κατά μήκος του σωλήνα με σταθερή μέση ταχύτητα.

Πυροσβεστικό όχημα – σωλήνας πυρόσβεσης

Οι πυροσβεστικοί εύκαμπτοι σωλήνες, που χρησιμοποιούνται σε πυρκαγιές μεγάλων κατασκευών, έχουν εγκάρσια διατομή A₁ = 32 cm². Ας υποθέσουμε ότι σε ένα τέτοιο σωλήνα το νερό ξεκινά με πίεση P₁ και με παροχή Π = 48 L/s. Ο εύκαμπτος αυτός σωλήνας φτάνει σε ύψος h = 10 m, πάνω σε μια τηλεσκοπική σκάλα ενός οχήματος πυρόσβεσης, και τελειώνει σε ένα ακροφύσιο που έχει εσωτερική διατομή A₂ = 8 cm².

α. Υποθέτοντας αμελητέες τις τριβές κατά την κίνηση του νερού στο σωλήνα, να υπολογίσετε την πίεση Ρ₁ του νερού στην αρχή του  σωλήνα.

Πυροσβεστήρας νερού

(Ένα εύκολο θέμα Β για τη γνωριμία με αυτού του είδους πυροσβεστήρα)

Σε έναν πυροσβεστήρα νερού, ο εγκλωβισμένος, υπό υψηλή πίεση αέρας, εξαναγκάζει το νερό να εκτοξεύεται από το ακροφύσιό του με μεγάλη ταχύτητα, όπως φαίνεται στο σχήμα. Θέτουμε σε λειτουργία έναν τέτοιο πυροσβεστήρα και διαπιστώνουμε ότι το νερό εκτοξεύεται με ταχύτητα v = 30 m/s όταν η στάθμη του νερού στο δοχείο είναι 0,5 m κάτω από το ακροφύσιο.

Από τα παραπάνω συμπεραίνουμε ότι η πίεση του αέρα μέσα στον πυροσβεστήρα είναι κατά

Σύγκριση των ισχύων δύο αντλιών, ένα Β΄ ΘΕΜΑ

Στο σχήμα διακρίνουμε μια αντλία νερού, στην οποία η διατομή του σωλήνα απορρόφησης νερού είναι Α₁=25 cm², ενώ η διατομή του σωλήνα στον οποίο οδηγείται το νερό είναι Α₂ = 10 cm².

Τα δύο μανόμετρα δείχνουν διαφορά πίεσης Ρ₂ – Ρ_1­ = 280 kPa, όταν η αντλία αντλεί το νερό με ρυθμό Π = 36m³/h. 

Να επιλέξετε, σε καθεμιά από τις τρεις προτάσεις που ακολουθούν, το σωστό και να αιτιολογήσετε την επιλογή σας.

Ι. Αν υ₁, υ₂ είναι οι ταχύτητες ροής του νερού  στους σωλήνες απορρόφησης και εκροής, αντίστοιχα, τότε για την ισχύ Ρ_αντλ της αντλίας ισχύει:

α) Ρ_αντλ = (Ρ₂– Ρ₁)Π + ½ρΠ(υ₂²– υ₁²),   β) Ρ_αντλ = (Ρ₂– Ρ₁)Π,    γ)  Ρ_αντλ = ½ρΠ(υ₂²– υ₁²)