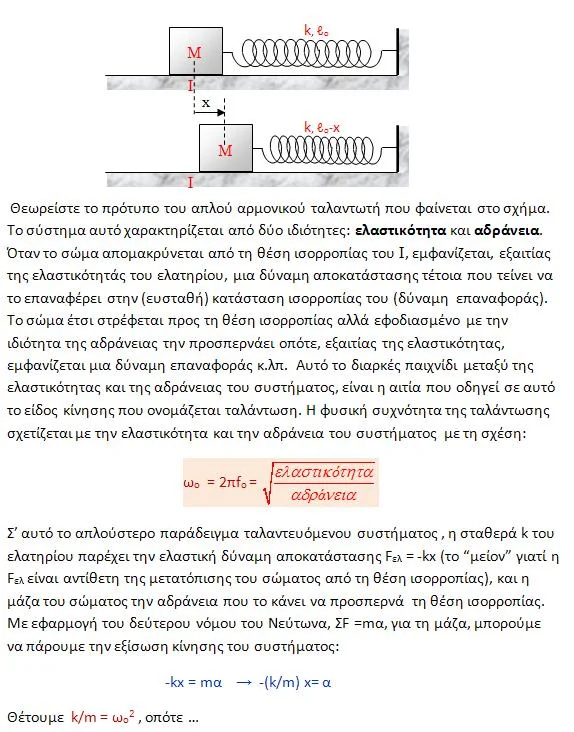
Kατά μήκος ενός γραμμικού ελαστικού μέσου, που η διεύθυνσή του
ταυτίζεται με τον άξονα x΄x, έχει αναπτυχθεί ένα
αρμονικό κύμα πλάτους Α. Θεωρούμε τη θέση ισορροπίας ενός σημείου Ο του
ελαστικού μέσου ως αρχή των αξόνων x΄x και
ψ΄ψ κι αρχίζουμε να μετράμε το χρόνο από κάποια στιγμή που το σημείο αυτό
βρίσκεται στην πάνω ακραία θέση του. Έτσι, τη στιγμή t = 0, στην αρχή αξόνων βρίσκεται η
κορυφή που δείχνεται με το κατακόρυφο βέλος.
α) Αν η ταχύτητα με την οποία
μετακινείται η κορυφή αυτή είναι υ = 1 m/sec και αν η μέγιστη επιτάχυνση του σημείου
Ο είναι 0,8π2 m/sec2,
να βρείτε την εξίσωση του κύματος.
β) Σε ποια θέση βρίσκεται η παραπάνω
κορυφή τη στιγμή που το σημείο Ο διέρχεται για έκτη φορά από τη θέση ισορροπίας
του;
(Τα παραπάνω στιγμιότυπα, για λόγους απλότητος, έχουν σχεδιαστεί σε ένα ορισμένο τμήμα του ελαστικού μέσου).