Στο χώρο αυτό, οι μαθητές της Γ Λυκείου αλλά και οι συνάδελφοι εκπαιδευτικοί θα βρουν μια σειρά από ερωτήσεις, πρωτότυπες ασκήσεις και προβλήματα στο πνεύμα των πανελλαδικών εξετάσεων. Το υλικό έχει ελεγχτεί και έχει πάρει την τελική του μορφή με τη συμβολή φίλων συνεργατών και ενός μεγάλου αριθμού μαθητών μου, μπορεί όμως ακόμη να έχει κάποιες ατέλειες. Οποιοδήποτε καλοπροαίρετο σχόλιο ή οποιαδήποτε διόρθωση είναι επιθυμητή.
Η φύση αγαπά την αλήθεια, και η αλήθεια της φύσης διεκδικεί το δικαίωμα να εκτίθεται μόνο σε όσους την ποθούν. Φ. Ντοστογιέφσκι
Δευτέρα 29 Ιανουαρίου 2018
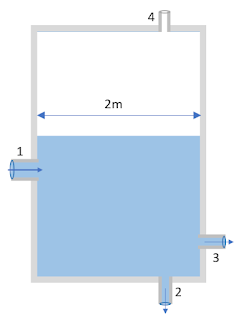
4. Ταχύτητα μετατόπισης στάθμης υγρού σε δεξαμενή κι εκτόπιση αέρα
Σάββατο 27 Ιανουαρίου 2018
3. Αιώρηση επίπεδης πλάκας πάνω σε πίδακα νερού
12. Υγρά σε ισορροπία. Ένα εύκολο αλλά πονηρό θέμα Β
Στο ανοικτό δοχείο περιέχονται δύο διαφορετικά μη αναμίξιμα υγρά Α και Β. Στη μια πλευρά του έχουν προσαρμοστεί δύο πιεσομετρητές (οι δύο σωλήνες Ι και ΙΙ που επικοινωνούν ο καθένας με το ένα από τα δύο υγρά). Οι αποστάσεις των δύο επιφανειών των υγρών από τη βάση του δοχείου είναι 2 m και 0,3 m Να υπολογίσετε
Παρασκευή 26 Ιανουαρίου 2018
2. Εκροή από κλειστό δοχείο
Πέμπτη 25 Ιανουαρίου 2018
1. Βεντουρίμετρο και παροχή
Σάββατο 20 Ιανουαρίου 2018
11. Έμβολα και ισορροπία (Απαιτούνται γνώσεις ισορροπίας στερεού)
Πέμπτη 18 Ιανουαρίου 2018
10ο. Εμβολο-στήριξη 2ο
Το αβαρές έμβολο εμβαδού Α = 10-3 m2 κλείνει
ερμητικά το κάτω μέρος ενός αβαρούς δοχείου γεμάτο με νερό μάζας m = 10 kg και
πυκνότητας ρ = 103 kg/m2, χωρίς αέρα, και δεν
εμφανίζει τριβές με τα τοιχώματα του δοχείου.
Το έμβολο στηρίζεται κατάλληλα σε σταθερό βάθρο. Στην πάνω βάση του δοχείου ασκούμε μια κατακόρυφη προς τα κάτω δύναμη F = 100 Ν.
Τετάρτη 17 Ιανουαρίου 2018
9. Εμβολο-στηρίξεις 1ο
Τα δύο αβαρή ισοϋψή δοχεία
περιέχουν ίδια ποσότητα νερού πυκνότητας ρ. Δεν περιέχουν αέρα. Κλείνονται
ερμητικά από αβαρή έμβολα, με εμβαδά Α1 και Α2
( Α1> Α2) που δεν εμφανίζουν τριβές με τα
δοχεία.
Τα έμβολα στηρίζονται κατάλληλα σε
σταθερό βάθρο.
Θέλουμε να συγκρίνουμε τις πιέσεις στα σημεία Ε και Δ.
8ο. Έμβολο + δύναμη + τρύπα στο δοχείο
Ι) Το μέτρο της F για να
μην μετακινείται το έμβολο πρέπει να είναι:
α) 2 Ν, β) 12 Ν,
γ) 10 Ν
ΙΙ) Η πίεση στο Ν είναι:
α) 1,2ˑ105 N/m2,
β) 2,2ˑ105 N/m2, γ) 2,1ˑ105 N/m2
Τρίτη 16 Ιανουαρίου 2018
7ο. Δύο έμβολα + δύο δυνάμεις
Δύο αβαρή έμβολα ίδιας κυκλικής
διατομής, εμβαδού Α, κλείνουν ερμητικά τα δύο στόμια του δοχείου του σχήματος,
που είναι γεμάτο με νερό. Η διάμετρός τους είναι ασήμαντη σε σχέση με τις
διαστάσεις του δοχείου, ώστε να μπορούμε να θεωρήσουμε ότι η πίεση στα σημεία
της εσωτερικής επιφάνειας του εμβόλου Ε2 είναι ίση με την πίεση
στο κέντρο του. Το δοχείο στηρίζεται ακλόνητα πάνω σε σταθερά υποστηρίγματα.
Ι. Αν Patm= 105N/m2, Α
= 10-4 m2, h = 2m, ρ= 103 kg/m3, g = 10 m/s2 και F1 = 10 N,
τότε για να ισορροπεί το σύστημα (δηλαδή να μην μετακινούνται τα έμβολα) πρέπει
η F2 να έχει μέτρο:
α) 11 Ν, β) 10 Ν,
γ) 12 Ν
ΙΙ) Η πίεση στο Ν είναι:
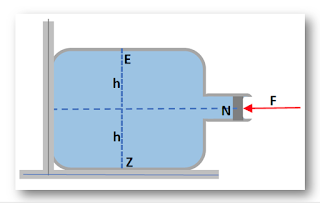
6ο. Έμβολο + δύναμη
Αν F = 2N, Patm = 105N/m2, h = 2m,
εμβαδό επιφάνειας εμβόλου Α = 10-4m2, πυκνότητα
υγρού ρ = 103 kg/m3 και g = 10 m/s2 τότε:
Ι) Η πίεση στο Ν θα είναι:
α) 105 N/m2,
β) 1,2ˑ105N/m2, γ) 1,4ˑ105N/m2
ΙΙ) Η πίεση στο Ε θα είναι:
α) 105 N/m2,
β) 1,2ˑ105N/m2, γ) 1,4ˑ105N/m2
ΙΙΙ) Η πίεση στο Ζ θα είναι:
α) 105 N/m2, β) 1,2ˑ105N/m2, γ) 1,4ˑ105N/m2
Δευτέρα 15 Ιανουαρίου 2018
5ο. Έμβολο + δύναμη, διάφοροι προσανατολισμοί.
4ο. Ένα έμβολο, διάφοροι
προσανατολισμοί.
Στο στόμιο ενός μπουκαλιού γεμάτο με νερό εισάγουμε
ένα αβαρές έμβολο εμβαδού Α, το οποίο μπορεί να γλιστράει χωρίς τριβές με τα
τοιχώματά του. Με τη βοήθεια κατάλληλης βαλβίδας αφαιρούμε τον αέρα που τυχόν
έχει εγκλωβιστεί, οπότε το έμβολο έρχεται σε επαφή με την ελεύθερη επιφάνεια
του νερού (σχήμα α). Στα σχήματα (β), (γ) και (δ) το ίδιο δοχείο το συγκρατούμε
σε πλάγια, οριζόντια και αντεστραμμένη, αντίστοιχα, θέση.
Ι) Πόση είναι η πίεση στα σημεία Α και Β σε κάθε
περίπτωση;
ΙΙ) Η δύναμη που ασκεί το νερό στο έμβολο στο σχήμα
(δ) είναι:
i. Ίση με το βάρος w του νερού.
ii. Ίση με W + PatmA
iii. Ίση με PatmA
3ο. Δύο ομοαξονικά έμβολα
Το δοχείο του σχήματος είναι γεμάτο με ιδανικό
υγρό και κλείνεται ερμητικά με δύο κυλινδρικά έμβολα Ε1 και Ε2 που
τα εμβαδά τους Α1 και Α2, αντίστοιχα, συνδέονται με
τη σχέση Α1 = 4Α2. Οι άξονες των δύο εμβόλων βρίσκονται
πάνω στην ίδια οριζόντια γραμμή, τη διακεκομμένη γραμμή του σχήματος σε
απόσταση h από την οροφή. Κάθετα στην επιφάνεια του εμβόλου Ε1 ασκούμε
δύναμη μέτρου F1, της οποίας ο φορέας ταυτίζεται με τον άξονα του
εμβόλου.
Ι) Για να παραμείνουν τα έμβολα ακίνητα στις αρχικές
τους θέσεις, πρέπει ταυτόχρονα στο έμβολο Ε2 να ασκήσουμε
κάθετη δύναμη στο κέντρο του, που έχει μέτρο F2 για το οποίο
ισχύει:
α. F2 =
4F1, β. F2 = F1,
γ. F2 = F1/4
ΙΙ) Η πίεση ΡΜ σε ένα σημείο Μ
της οριζόντιας γραμμής των αξόνων των δύο εμβόλων είναι:
α. ΡΜ= F1/A1 ή ΡΜ = F2/A2, β. ΡΜ= F1/A1+F2/A2, γ. ΡΜ=
F1/A1+ Ρatm
ΙΙΙ) Αν στα σημεία της οροφής επικρατεί πίεση ίση με Patm τότε:
α. F1 = (Patm – ρgh)Α1, β. F1 = ρghΑ1, γ. F1 = (Patm + ρgh)Α1
Κι άλλα έμβολα σε δοχεία με υγρά - Αρχή του Pascal.
2ο. Δύο έμβολα, δύο δυνάμεις, στο
κενό χωρίς βαρύτητα.
Το δοχείο του πλαϊνού σχήματος
βρίσκεται εκτός πεδίου βαρύτητας και εκτός ατμόσφαιρας. Είναι γεμάτο με νερό το
οποίο συμπιέζεται από τις δυνάμεις F, που ενεργούν κάθετα στα δύο
αντικριστά στεγανά έμβολα ίδιας διατομής Α, τα οποία ισορροπούν. Η πίεση στο σημείο
Μ που βρίσκεται στην ευθεία των κοινών αξόνων των δύο εμβόλων και ισαπέχει από
αυτά είναι:
α) μηδέν,
β) F/A,
γ) 2F/A
Επιλέξτε το σωστό και αιτιολογείστε.