Διορθωμένες Εκφωνήσεις - Απαντήσεις Τράπεζας Θεμάτων Φυσικής Γ΄ ΛΥΚΕΙΟΥ.

Ο Τρίτος τόμος της εξαιρετικής δουλειάς του συνάδελφου Δημήτρη Ζωγράφου

ΕΔΩ

ΚΒΑΝΤΙΚΗ ΘΕΩΡΙΑ ΓΙΑ ΥΠΟΨΗΦΙΟΥΣ

 Μια ελκυστική παρουσίαση της θεωρίας του κεφαλαίου της Κβαντικής Φυσικής, όπως διδάσκεται στα σχολεία των ΗΠΑ. Περιέχει και εβδομήντα τρεις ασκήσεις. 

[Κάνετε κλικ πάνω στην εικόνα]

Κύρια πηγή: Physics: principles and problems

Δεύτερη Πηγή: Physics: Raymond A. Serway  John W. Jewett, Jr.

Tράπεζα θεμάτων φυσικής Β Λυκείου

Νέα τράπεζα θεμάτων φυσικής Β Λυκείου ανά κεφάλαιο,  μαζί με τις λύσεις τους, ταξινομημένα με διαβαθμισμένη δυσκολία. Ένα καλαίσθητο πλήρες πόνημα, ευγενική προσφορά του συναδέλφου Λάμπρου Αδάμ.

           

                                                             

  ΘΕΜΑ Β

 

         

   ΘΕΜΑ Δ

Τράπεζα θεμάτων φυσικής Α Λυκείου

 Νέα τράπεζα θεμάτων φυσικής Α Λυκείου (2023) μαζί με τις λύσεις τους ανά κεφάλαιο, ταξινομημένα με διαβαθμισμένη δυσκολία. Ένα καλαίσθητο πλήρες πόνημα του συναδέλφου Λάμπρου Αδάμ

ΘΕΜΑ Α

ΘΕΜΑ Β

ΘΕΜΑ Γ                       ΘΕΜΑ Δ

  

Θεωρητικά σημειώματα Κβαντομηχανικής

 

Σημειώσεις Κβαντομηχανικής(από Ψ.Ε.Β.)

Η Παγκοσμιότητα της "ακτινοβολίας μαύρου σώματος"

 Το χρονικό  της ακτινοβολίας μαύρου σώματος

Μαύρο χρώμα έχουν τα σώματα που απορροφούν, χωρίς να ανακλούν, όλα τα μήκη κύματος της ακτινοβολίας που πέφτει πάνω τους. Είναι δηλαδή τέλειοι απορροφητές ακτινοβολίας. Τι είναι, λοιπόν, η ακτινοβολία μαύρου σώματος; Αν το μαύρο σώμα είναι τέλειος απορροφητής τότε γιατί εκπέμπει ηλεκτρομαγνητική ακτινοβολία; 

Όλο το "χρονικό" εδώ:

🌐 Θέλεις περισσότερη Φυσική;

Μπες στο Global Physics Entrance Portal και βρες υλικό για κρούση, ταλαντώσεις, κύματα, στερεό σώμα, ηλεκτρομαγνητισμό, ρευστά, κβαντομηχανική.

➤ Go to Portal

Το "μαύρο" φως των Αστεριών

 

Το φως των αστεριών είναι μέρος της ακτινοβολίας που είναι εγκλωβισμένη στη  φωτόσφαιράς τους, σε θερμική ισορροπία με το ρευστό υλικό της. Ένα μέρος της ακτινοβολίας αυτής εξέρχεται από την εξωτερική επιφάνεια της φωτόσφαιρας, διαπερνά την ατμόσφαιρα του άστρου, γνωστή ως χρωμόσφαιρα,  και διαφεύγει στο διάστημα ως ακτινοβολία σχεδόν^[1] μαύρου σώματος. (Είναι προφανής η αντιστοιχία θερμοδυναμικής ισορροπίας ύλης - ακτινοβολίας στο εσωτερικό της φωτόσφαιρας με την αντίστοιχη ισορροπία στο εσωτερικό του κουτιού του Kirchhoff, και της επιφάνειας της φωτόσφαιρας με την τρύπα του κουτιού απ’ όπου εξέρχεται η ακτινοβολία).

Κατεβάστε όλο το άρθρο από εδώ:

---

[1] Μετά την αφαίρεση κάποιων αλλοιώσεων, που οφείλονται στην απορρόφηση ορισμένων μηκών κύματος από στοιχεία στην ατμόσφαιρα του άστρου, στη διαστρική ύλη και στη σχετική κίνηση η οποία μετατοπίζει το φάσμα προς το ερυθρό ή το κυανό. Αυτές απαλείφονται με τη βοήθεια υπολογιστή. Αν η μέτρηση δεν γίνει έξω από την ατμόσφαιρα (δηλαδή, από δορυφόρο) γίνεται απαλοιφή και της ατμοσφαιρικής δράσης στην ακτινοβολία του άστρου.

Ολο το Σύμπαν, ένα κουτί του Kirhhoff

   Tο παρατηρήσιμο σύμπαν σε όλο και πιο συμπαγή κλίμακα. Η Γη και ο Ήλιος βρίσκονται στο κέντρο, ακολουθούμενοι από το ηλιακό μας σύστημα, μετά τα κοντινά αστέρια , οι κοντινοί γαλαξίες, οι μακρινοί γαλαξίες, τα νημάτια της πρώιμης ύλης και τελικά το κοσμικό υπόβαθρο μικροκυμάτων.

  Το φάσμα του κοσμικού υπόβαθρου μικροκυμάτων (CMB), μιας αχνής, σήμερα, λάμψης του αρχέγονου φωτός της Δημιουργίας, είναι ακριβώς το σχήμα μιας καμπύλης μαύρου σώματος που εκπέμπεται από ένα αδιαφανές κέλυφος με θερμοκρασία 2,725 Kelvin.

Όλο το άρθρο εδώ:

Ακτινοβολία "Γκρίζου" σώματος

Για να ισχύουν οι νόμοι που διέπουν την ακτινοβολία μαύρου σώματος σε πραγματικά σώματα, έχει εισαχθεί η έννοια του «γκρίζου σώματος» και της «ακτινοβολίας γκρίζου σώματος». Είναι ένα ιδανικό αδιαφανές σώμα, πολύ πιο κοντά στο πραγματικό απ’ ότι το μαύρο σώμα, που η ικανότητα εκπομπής του ε_g (άρα και η απορροφητικότητά του α_g)  εξαρτάται μόνο από τις φυσικές ιδιότητες του σώματος -δεν αλλάζει με τη θερμοκρασία και είναι σταθερή για όλα τα μήκη κύματος.

Περισσότερα...

Ακτινοβολία μαύρου σώματος

  Προσομοίωση του φάσματος εκπομπής του μαύρου σώματος σε διάφορες θερμοκρασίες -από το Phet. (Κάντε κλικ στην εικόνα)

Η ΔΥΑΔΙΚΗ ΦΥΣΗ ΤΟΥ ΦΩΤΟΣ

Μέσα σε 4 λεπτά αυτό το βίντεο συνοψίζει όλο το κεφάλαιο της Κβαντομηχανικής της Γ Λυκείου

Τράπεζα Β και Δ θεμάτων (2022-2025) της Γ΄ Λυκείου μαζί με τις λύσεις τους

Διαρκώς ενημερούμενη τράπεζα με Θέματα Β και Δ της Γ΄ Λυκείου, μαζί με τις λύσεις τους, ταξινομημένα με διαβαθμισμένη δυσκολία. Ένα καλαίσθητο πλήρες πόνημα του συναδέλφου Λάμπρου Αδάμ.

ΘΕΜΑ Β

ΘΕΜΑ Δ

Επίσης από τον ίδιο, ανάλογη παρουσίαση:

 των θεμάτων Β και Δ της Β Λυκείου και των 

θεμάτων      Α   -   Β  -   Γ   -   Δ  και  της Α Λυκείου 2021-2022 

(κάντε κλικ πάνω στα γράμματα Α, Β,  Γ, και Α-Γ κάθε τάξης)

Επαγωγικό ρεύμα σε κυκλικό αγώγιμο βρόχο

"Το επαγωγικό ρεύμα σε κυκλικό αγώγιμο βρόχο, εντός ομαλά μεταβαλλόμενου Μ.Π., εξαρτάται μόνο από τη μάζα και από τη φύση του υλικού του"

Τα δύο χάλκινα δακτυλίδια στα σχήματα α και β, με διαφορετικές διαμέτρους D₁ και D₂ και διαφορετικές διατομές Α₁ και Α₂, έχουν ίδια μάζα m. Το καθένα βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο με την επιφάνειά του κάθετη προς τις δυναμικές του γραμμές. Αν η ένταση κάθε μαγνητικού πεδίου μεταβάλλεται με σταθερό ρυθμό έτσι ώστε dB₁/dt = dB₂/dt = λ, σε ποιο δακτυλίδι αναπτύσσεται μεγαλύτερο επαγωγικό ρεύμα;

Δίνεται ότι η ωμική αντίσταση ενός ομογενούς αγωγού σταθερής διατομής παρέχεται από τη σχέση R = ρℓ/Α, όπου ρ η ειδική αντίστασή του, ℓ το μήκος του και Α η διατομή του.

Γιατί στο νόμο της επαγωγής του Faraday δεν λαμβάνουμε υπόψη και τη μαγνητική ροή του επαγόμενου ρεύματος;

Ερώτηση μαθητή: 

"Σε μια θέση που χαρακτηρίζεται από γωνία φ, η μαγνητική ροή στο πλαίσιο προέρχεται εν μέρει από το εξωτερικό πεδίο με σταθερή ένταση Β και εν μέρει από το μαγνητικό πεδίο του επαγόμενου ρεύματος. Γιατί στο νόμο της επαγωγής του Faraday δεν λαμβάνουμε υπόψη και τη μαγνητική ροή του επαγόμενου ρεύματος;"

Το πρότυπο του απλού αρμονικού ταλαντωτή

Η συνέχεια του θεωρητικού σημειώματος σε pdf εδώ

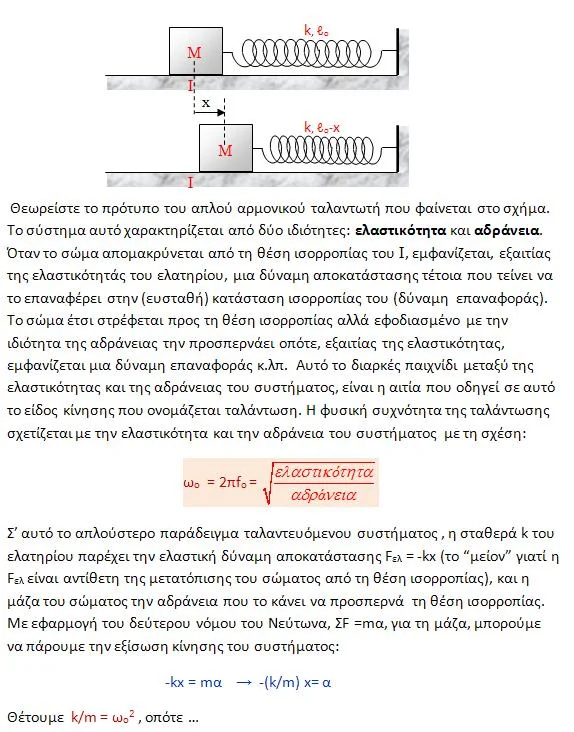
Απλή αρμονική ταλάντωση συστήματος "ιδανικού κατακόρυφου ελατηρίου - μάζας" σε πεδίο βαρύτητας

   Το παρακάτω άρθρο, είναι η συνέχεια της ανάρτησης  "το πρότυπο του απλού αρμονικού ταλαντωτή". Είχε δημοσιευτεί πέρσι τον Αύγουστο. Το ξαναδίνω αναθεωρημένο στην κυκλοφορία σε τέσσερα μέρη και εμπλουτισμένο με δύο σχετικές ασκήσεις. 

• Το πρώτο μέρος είναι αρκετά τυπικό και περιέχει βασικές γνώσεις α.α.τ. 
• Το δεύτερο περιγράφει πώς δυο καλοί μαθητές μπορούν εύκολα να μπλέξουν "σαν τον Ηρακλή με τις κουβαρίστρες", ακριβώς επειδή είναι καλοί. Ευτυχώς που είναι δύο! 
• Στο τρίτο μέρος οι συμμαθητές "γεννούν" μια ιδέα που ξεκαθαρίζει τη σχέση μεταξύ των τριών δυναμικών ενεργειών: βαρύτητας, ελαστικότητας και ταλάντωσης. 
• Στο τέταρτο μέρος γίνεται αναλυτική παρουσίαση δύο σχετικών ασκήσεων.

Το άρθρο διαβάζεται εύκολα και από μαθητές. Απαιτεί, ίσως, λίγο παραπάνω συγκέντρωση, θα ωφεληθούν όμως και κάποια από αυτά ίσως τα βρουν μπροστά τους!

• ΜΕΡΟΣ 1^ο: Τα βασικά (μαζί με μια εφαρμογή)

• ΜΕΡΟΣ 2^ο:  Όπου δυο μαθητές, προσπαθούν να δώσουν απάντηση σε μια απλή αλλά ενδιαφέρουσα ερώτηση. 

• ΜΕΡΟΣ 3^ο: Όπου οι δυο μαθητές κάνουν μια "σημαντική ανακάλυψη" για τη Μηχανική ενέργεια ταλάντωσης συστήματος "κατακόρυφου ελατηρίου – μάζας".

• ΜΕΡΟΣ 4^ο: Όλες οι δυναμικές ενέργειες μαζί. (Δύο ασκήσεις με τη λύση τους)

Ένα θέμα Β που προκάλεσε σύγχυση στους υποψήφιους φοιτητές στην Ινδία.

Είναι ίσως η πιο “μπερδευτική” ερώτηση που έχει μπει σε εισαγωγικές εξετάσεις· συγκεκριμένα, στις εξετάσεις του JEE Advance, που θεωρείται διεθνώς ως μία από τις πιο δύσκολες και αντικειμενικές εξετάσεις εισαγωγής⁽¹⁾ σε προπτυχιακά προγράμματα διαφόρων κολεγίων και ανωτάτων σχολών στην Ινδία ⁽²⁾. 

Τι είναι πιο εύκολο, να σπρώξουμε ένα σώμα ή να το τραβήξουμε;

Η ερώτηση είναι, βασικά, απλή και οποιοσδήποτε χωρίς πολλές γνώσεις φυσικής μπορεί να την απαντήσει, προκάλεσε όμως πονοκέφαλο στους υποψήφιους.

Ας δούμε μια απάντηση:

Αξιοποιώντας την στροφορμή και την κινητική ενέργεια λόγω περιστροφής

Ο σφόνδυλος είναι μια μάζα, περιστρεφόμενη γύρω από ακλόνητο άξονα, η οποία μπορεί να αποθηκεύσει ενέργεια με μηχανικό τρόπο, υπό τη μορφή κινητικής ενέργειας λόγω περιστροφής. 

Σήμερα, συνδυάζεται με μια ηλεκτρική συσκευή, που μπορεί να λειτουργεί άλλοτε ως κινητήρας και άλλοτε ως γεννήτρια. Όταν η ηλεκτρική συσκευή λειτουργεί ως κινητήρας, θέτει σε περιστροφή τον σφόνδυλο και όσο πιο γρήγορα περιστρέφεται αυτός, τόσο περισσότερη ενέργεια αποθηκεύει. Ο σφόνδυλος, δηλαδή, λειτουργεί ως συσσωρευτής μηχανικής ενέργειας.

Πού πήγε η ενέργεια που χάθηκε; (Απορία μαθητή)

Απορία μαθητή. Μου δόθηκε η εξής άσκηση:

Η ράβδος του σχήματος είναι οριζόντια και μπορεί να στρέφεται γύρω από κατακόρυφο άξονα που διέρχεται από το μέσον της. Το μήκος της ράβδου είναι L και η μάζα της Μ. Σε απόσταση r από τον άξονα περιστροφής βρίσκονται δύο μεταλλικοί δακτύλιοι μάζας m, ο καθένας, που συνδέονται μεταξύ τους με ένα νήμα. Το σύστημα στρέφεται γύρω από τον άξονα με γωνιακή συχνότητα ω₀. Κάποια στιγμή το νήμα σπάει και οι δακτύλιοι, λόγω αδράνειας, ωθούνται στα άκρα της ράβδου, όπου δεν υπάρχει κανένα εμπόδιο να τους συγκρατήσει κι έτσι πέφτουν στο έδαφος. Να υπολογίστε τη γωνιακή ταχύτητα του συστήματος και την κινητική ενέργεια περιστροφής του, τη στιγμή που οι δύο δακτύλιοι φτάνουν στο τέλος της ράβδου. Η ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το κέντρο μάζας της είναι  I_ρ = ML²/12.

Γνωρίζω ότι πρέπει να χρησιμοποιήσω την αρχή διατήρησης στροφορμής:

                                         Ι₀ω₀ = Ι_τελω_τελ (=L) →  ω_τελ = Ι₀ω₀/Ι_τελ

Και επομένως: 

                                             ΔΚ_σροφ =  (1/2)Lω_τελ - (1/2)Lω₀ < 0,

δηλαδή, έχουμε απώλεια ενέργειας.

Έχω όμως τις εξής απορίες:

1. Δεν έχουμε εξωτερικές δυνάμεις και ροπές στο σύστημα. Γιατί παραβιάζεται εδώ η αρχή διατήρησης της ενέργειας:

                                                       (1/2)Ι₀ω₀² =  (1/2)Ι_τελω_τελ²

Απ’ όπου προκύπτει αποτέλεσμα:  ω_τελ = ω₀√( Ι₀/Ι_τελ) < ω₀  και ΔΚ = 0, εντελώς διαφορετικό; Πού πήγε η ενέργεια που χάθηκε;

2. Όταν οι δακτύλιοι φύγουν από τη ράβδο, η νέα της γωνιακή ταχύτητα θα υπολογιστεί από τη σχέση 

                                           Ι_ρ· ω_νεα = (Ι_ρ+ 2mL²/4) ω_τελ;

Απάντηση:

Είναι μια όμορφη απορία, που απ' την εμπειρία μου γνωρίζω ότι την έχουν και άλλοι μαθητές. 

Ας πάρουμε ένα-ένα τα ερωτήματα:

1. Δεν παραβιάζεται η αρχή διατήρησης της μηχανικής ενέργειας!

Στην εξίσωσή σου  (1/2)Ι₀ω₀² =  (1/2)Ι_τελω_τελ²,  θεωρείς ότι το σύστημα, τόσο στην αρχική όσο και στην τελική του κατάσταση, έχει μόνο κινητική ενέργεια λόγω περιστροφής. Όμως, υπάρχει και μια ποσότητα κινητικής ενέργειας  λόγω μεταφορικής κίνησης των δακτυλίων, καθώς αυτοί οδηγούνται, λόγω αδράνειας, προς τα άκρα της ράβδου. Οι δακτύλιοι, και περιστρέφονται και μετατοπίζονται, κι έτσι η συνολική τους ταχύτητα δεν είναι ίδια με την ταχύτητα των σημείων της ράβδου πάνω στα οποία εφάπτονται.

Πρέπει λοιπόν να διορθωθεί η προηγούμενη σχέση στην εξής

                                    (1/2)Ι₀ω₀² =  (1/2)Ι_τελω_τελ²+ 2(1/2)mυ_δ²    (1)

Όπου υ_δ είναι η ταχύτητα λόγω μεταφορικής κίνησης με την οποία φτάνουν οι δακτύλιοι στα άκρα της ράβδου.

Έτσι, στην εξίσωση (1) της Α.Δ.Μ.Ε υπάρχουν δύο άγνωστοι, το ω_τελ και η υ_δ και άρα, αφού το σύστημα είναι μονωμένο, πρέπει να καταφύγεις και σε μια άλλη αρχή διατήρησης, αυτή της Α.Δ.Σ   (Ι₀ω₀ = Ι_τελω_τελ), απ’ όπου άμεσα προκύπτει το ω_τελ. Ύστερα, από την εξίσωση (1), μπορείς να υπολογίσεις και την (ακτινική) ταχύτητα  με την οποία φτάνουν οι δακτύλιοι στα άκρα της ράβδου.

2.  Όχι. Όταν οι δακτύλιοι εγκαταλείψουν τη ράβδο, αυτή θα συνεχίσει να κινείται με γωνιακή ταχύτητα ω_τελ, (ίση με αυτήν που είχε το σύστημα, τη στιγμή που οι δακτύλιοι έφταναν στα άκρα της ράβδου).

Η εξήγηση είναι απλή:  Μπορεί οι δακτύλιοι να εγκαταλείπουν τη ράβδο, κρατάνε ίδια όμως τη στροφορμή τους, αφού δεν δέχονται κάποια εξωτερική ροπή. Πρέπει όμως να κρατήσει ίδια τη στροφορμή της και η ράβδος, αφού το σύστημα είναι μονωμένο, και αυτό σημαίνει ότι δε θα αλλάξει η γωνιακή της ταχύτητα.  

Στη σχέση, που γράφεις, έχεις παραλείψει τη στροφορμή που έχουν οι δακτύλιοι όταν εγκαταλείψουν τη ράβδο. Πρέπει να διορθωθεί στην εξής:

                         Ι_ρ· ω_νεα + (2mL²/4) ω_τελ = (Ι_ρ+2mL²/4) ω_τελ 

Είναι φανερό ότι από αυτήν προκύπτει ω_νεα = ω_τελ.

 

Παρατήρηση: Υπόψη ότι, επειδή το σύστημα είναι μονωμένο, δεν συνεπάγεται ότι έχουμε και διατήρηση της μηχανικής του ενέργειας. Αυτό ισχύει μόνο αν οι δυνάμεις μέσα σε αυτό είναι συντηρητικές.  Υπάρχει, για παράδειγμα, η άσκηση 4.60 του σχολικού βιβλίου. Εκεί οι δακτύλιοι σταματάνε στα εμπόδια που υπάρχουν στα δύο άκρα της ράβδου. Είναι φανερό ότι στην άσκηση αυτή δεν ισχύει η Α.Δ.Μ.Ε, αφού οι δακτύλιοι συγκρούονται με τα εμπόδια και θεωρούμε ότι παραμένουν εκεί (πλαστική κρούση). Όλη η κινητική τους ενέργεια λόγω της ακτινικής τους ταχύτητας μετατρέπεται σε θερμική. Όταν όμως το σύστημα είναι μονωμένο, ισχύει πάντα η αρχή διατήρησης της στροφορμής του.

Η απάντηση στο παράδοξο της συνολικής στροφορμής δύο δίσκων

Δεν έχουμε εδώ διατήρηση της στροφορμής του συστήματος των δύο δίσκων. Αν ίσχυε, θα είχαμε: Ι₁ω₀ = Ι₁ω₁ – Ι₂ω₂, δηλαδή Ι₁ω₁ = Ι₁ω₀ + Ι₂ω₂, οπότε ω₁ > ω₀ και άρα η κινητική ενέργεια κάθε δίσκου θα αύξαινε, άρα και του συστήματος. Φυσικά, αυτό αντίκειται στην Α.Δ.Ε. συστήματος.

Τι συμβαίνει λοιπόν; 

Κοιτάξτε το αριστερό σχήμα (α): Θεωρήστε τους δύο δίσκους πάνω σε λείο οριζόντιο επίπεδο. Είναι η στιγμή που φέρνουμε σε επαφή τις περιφέρειες των  δύο δίσκων. Έχουν σχεδιαστεί οι δύο τριβές ολίσθησης (με κόκκινο χρώμα) στις περιφέρειες των δύο δίσκων. Είναι δύο δυνάμεις αντίθετες (δράση – αντίδραση), που δρουν στα σημεία επαφής των περιφερειών των δύο δίσκων. Επειδή οι εξωτερικές δυνάμεις, βάρος -  αντίδραση δαπέδου, έχουν συνισταμένη μηδέν, κάθε δίσκος δέχεται μια καθαρή δύναμη Τ, που παρουσιάζει ροπή ως προς το κέντρο μάζας του. Το αποτέλεσμα είναι γνωστό: Ο δίσκος 2 θα εκτελέσει μια σύνθετη κίνηση, μεταφορική κατά τη διεύθυνση της Τ και στροφική γύρω από το κέντρο μάζας του, κατά τη φορά της ροπής της Τ. Αντίστοιχα, ο δίσκος 1 θα εκτελέσει και αυτός μια μεταφορική κίνηση κατά τη φορά της Τ, ενώ η στροφική κίνηση θα περιοριστεί και θα μειωθεί (λόγω της ροπής της Τ) η γωνιακή του ταχύτητα. Έτσι, σε ελάχιστο χρονικό διάστημα, οι δύο δίσκοι θα απομακρυνθούν κινούμενοι όπως στο σχήμα (β).

Όμως, στο πρόβλημά μας, υπάρχουν δύο ακλόνητοι άξονες περιστροφής κάθετοι στα κέντρα των δύο δίσκων   και, όπως φαίνεται από την παραπάνω ανάλυση, αυτοί οι δύο άξονες δε θα επιτρέψουν τη μεταφορική κίνηση των δύο δίσκων. Πρέπει, λοιπόν, στη διάρκεια που οι δύο περιφέρειες ασκούν τριβή η μία στην άλλη, ο άξονας κάθε δίσκου να ασκεί δύναμη αντίθετη της τριβής που δέχεται, (στο σχήμα γ φαίνονται με μπλε χρώμα), ώστε να ισχύει σε καθένα δίσκο η συνθήκη ΣF = 0*. 

Οι δυνάμεις αυτές των αξόνων είναι εξωτερικές δυνάμεις, και για το σύστημα των δύο δίσκων αποτελούν ζεύγος εξωτερικών δυνάμεων. Αν γνωρίζουμε τις τριβές Τ, τότε στο σύστημα των δύο δίσκων ενεργεί μια εξωτερική ροπή -Τ(r₁ + r₂) κατά τη φορά των δεικτών του ρολογιού (αρνητική).

Επειδή η εξωτερική ροπή έχει φορά αντίθετη από την αρχική στροφορμή του συστήματος, η στροφορμή του συστήματος μειώνεται.

* Ουσιαστικά, η ροπή Tr₁ ή Tr₂, σε κάθε δίσκο, είναι η ροπή του ζεύγους των δυνάμεων Τ που ενεργεί σε καθένα από αυτούς.

Στο σύστημα των δύο δίσκων ενεργούν, επίσης, και άλλα δύο ζεύγη δυνάμεων με μηδενική ροπή, αφού οι άξονές τους ταυτίζονται. Είναι οι οριζόντιες δυνάμεις Ν με τις οποίες οι άξονες κρατούν σε επαφή τους δύο δίσκους (οι κόκκινες, που είναι εσωτερικές στο σύστημα των δύο δίσκων, απαραίτητες για την εμφάνιση των τριβών, Τ = μΝ) και οι μπλε που είναι εξωτερικές δυνάμεις από τους δύο άξονες προς τους δίσκους, με συνισταμένη μηδέν.  

Είναι, λοιπόν, φανερό ότι δεν μπορούμε να εφαρμόσουμε καμία από τις αρχές διατήρησης (ενέργειας ή στροφορμής).

Τότε, πώς θα λύσουμε την άσκηση;

Μόνο με τη βοήθεια του θεμελιώδη νόμου της στροφικής κίνησης:

Έστω Δt το χρονικό διάστημα ολίσθησης των περιφερειών των δύο δίσκων. Όταν οι περιφέρειες σταματήσουν να ολισθαίνουν μεταξύ τους, τότε τα σημεία επαφής τους θα έχουν ίσες ταχύτητες (υ₁ = υ₂  → ω₁r₁ = ω₂r₂) και έτσι θα σταματήσουν να τρίβονται μεταξύ τους (Τ = 0).

Για κάθε δίσκο ο θεμελιώδης νόμος της στροφικής κίνησης (Στ = ΔL/Δt) παίρνει τη μορφή:

                                 -Τr₁ = I₁(ω₁ – ω₀)/Δt,   για τον δίσκο 1, και

                                  Τr₂ = I₂(ω₂ – 0)/Δt,     για το δίσκο 2

Διαιρούμε:                 

                                  - r₁/r₂ = [I₁(ω₁ – ω₀)]/I₂ω₂

Από την ισότητα των ταχυτήτων προκύπτει ότι ω₂ = ω₁r₁/r₂ και αν θέσουμε αυτή την τιμή του ω₂ στην παραπάνω σχέση, θα βρούμε τελικά:

                                      ω₁ = (Ι₁ω₀)/[Ι₁ + (r₁/r₂)²I₂]