Κύλιση τροχού με σταθερή επιτάχυνση σε παράλληλες σιδηροτροχιές

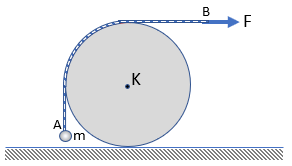
Ένα αβαρές, μη εκτατό σχοινί, είναι περασμένο στο αυλάκι μιας αβαρούς τροχαλίας Π, που μπορεί να περιστρέφεται χωρίς τριβές γύρω από ακλόνητο οριζόντιο άξονα και στη συνέχεια είναι τυλιγμένο πολλές φορές στην περιφέρεια ενός ομογενούς τροχού T ακτίνας R, που μπορεί να περιστρέφεται μαζί με τον άξονά του, ο οποίος είναι ένας αβαρής κύλινδρος ακτίνας R/2 σταθερά συνδεμένος με αυτόν. Ο κυλινδρικός άξονας του τροχού, μπορεί να κυλήσει χωρίς ολίσθηση κατά μήκος δύο οριζόντιων παράλληλων σιδηροτροχιών P, (επειδή στο σχήμα α φαίνεται μόνο η σιδηρογραμμή στην μπροστινή όψη του τροχού, στο σχήμα β παρατίθεται σχετική κάτοψη). Η μάζα του τροχού είναι Μ και  η ροπή αδράνειάς του ως προς τον νοητό άξονα που είναι κάθετος στο κέντρο C του τροχού είναι (1/2)ΜR². Αν το άκρο Λ του σχοινιού τραβιέται προς τα κάτω με σταθερή επιτάχυνση g/2 και το σχοινί δεν ολισθαίνει καθώς ξετυλίγεται, να βρείτε:

α) Την κατεύθυνση προς την οποία θα κινηθεί το κέντρο C του τροχού.

β) Την επιτάχυνση του κέντρου C.

γ) Την κατεύθυνση και το μέτρο της τριβής μεταξύ της επιφάνειας του κυλινδρικού άξονα και των σιδηροτροχιών.

δ) Την τάση του σχοινιού.

Απάντηση σε pdf:  
Απάντηση σε word:

Πλαίσιο, μαγνητικό πεδίο, ρεύμα, σχοινιά και τάσεις

Ένας ομοιόμορφος (ομογενής και ισοπαχής) ορθογώνιος βρόχος με μήκη πλευρών d,ℓ (d < ℓ) και με μάζα m κρέμεται οριζόντια με τη βοήθεια δύο κατακόρυφων σχοινιών. Ο βρόχος διαρρέεται από ρεύμα i και βρίσκεται μέσα σε ένα ομογενές οριζόντιο μαγνητικό πεδίο Β το οποίο είναι παράλληλο με τη μακρύτερη πλευρά του.

H τάση του σχοινιού που είναι δεμένο στο σημείο Α είναι:

                             α) mg – Bid,    β) mg/2 – Bid,     γ) mg/2 +Bid

Να επιλέξετε με αιτιολόγηση την ορθή σχέση. 

Απάντηση σε pdf:  
Απάντηση σε word:

Επιτάχυνση του σημείου επαφής τροχού – κυρτής επιφάνειας

 Μια κυρτή επιφάνεια έχει ομοιόμορφη ακτίνα καμπυλότητας ίση με 6R. Ένας τροχός ακτίνας R κυλίεται χωρίς να ολισθαίνει πάνω της με ταχύτητα υ σταθερού μέτρου. Η επιτάχυνση των σημείων του τροχού ως προς το κέντρο Ο της κυρτής επιφάνειας, τη στιγμή που έρχονται σε επαφή με αυτήν, έχει μέτρο:

                                                    α) 6υ²/7R,     β) 5υ²/6R,     γ) μηδέν 

Απάντηση σε pdf: 
Απάντηση σε word:

Η προφανής και η «αφανής» στατική τριβή στη μη ολίσθηση

Στο σχήμα φαίνεται η εγκάρσια κατακόρυφη τομή ενός οριζόντιου ομογενούς κυλίνδρου, που το κέντρο της ταυτίζεται με το κέντρο μάζας του κυλίνδρου. Ένα μικρό σώμα μάζας m κρατιέται σε ισορροπία δεμένο στην άκρη Α ενός σχοινιού αμελητέας μάζας, του οποίου ένα τμήμα εφάπτεται στον κύλινδρο, όπως φαίνεται στο σχήμα. Η άλλη άκρη B του σχοινιού τραβιέται από μια οριζόντια δύναμη F. Αν το σχοινί δεν ολισθαίνει στην επιφάνεια του κυλίνδρου και ο κύλινδρος ηρεμεί στην οριζόντια επιφάνεια, το μέτρο της F είναι ίσο με:

                                       α)  mg/2            β) mg,             γ)  3mg/2

Σύντομη απάντηση: 
Αναλυτική απάντηση σε pdf: 
Αναλυτική απάντηση σε word:

Περιστροφή δίσκου γύρω από οριζόντια χορδή του

Ένας ομογενής κυκλικός δίσκος έχει ακτίνα R και μάζα m. Ένα σωματίδιο, επίσης μάζας m, είναι στερεωμένο στο σημείο Σ στην άκρη του δίσκου όπως φαίνεται στο σχήμα. Ο δίσκος μπορεί να περιστρέφεται χωρίς τριβές γύρω από τον σταθερό οριζόντιο άξονα ΡΡ΄, πάνω στον οποίο βρίσκεται η χορδή ΑΒ που απέχει R / 4 από το κέντρο Κ του δίσκου και είναι κάθετη στην προέκταση της ακτίνας ΣΚ. Αρχικά, ο δίσκος κρατείται κατακόρυφα με το σωματίδιο στο σημείο Σ στην υψηλότερη θέση του. Στη συνέχεια αφήνεται να πέσει, έτσι ώστε να αρχίσει να περιστρέφεται γύρω από τοnν άξονα PΡ΄. 

Βρείτε τη γραμμική ταχύτητα του σωματιδίου καθώς φθάνει στη χαμηλότερη θέση του.

Δίνεται ότι η ροπή αδράνειας ομογενούς κυκλικού δίσκου ως προς άξονα που βρίσκεται στο επίπεδό του και διέρχεται από το κέντρο του είναι I = mR²/4. 

Απάντηση σε pdf 
Απάντηση σε word:

Κατακόρυφη περιστροφή ράβδου στο εσωτερικό κοίλου κυλίνδρου

[Εδώ, μια ράβδος στρέφεται γύρω από άξονα που δεν διέρχεται από το φορέα της]

Θεωρείστε ένα κοίλο κύλινδρο σταθερό σε οριζόντιο επίπεδο, με λεία εσωτερική επιφάνεια ακτίνας     R = 5 m και μια ομογενή ράβδο μάζας M και μήκους L = 8 m, που συγκρατείται αρχικά σε κατακόρυφη θέση όπως φαίνεται στο σχήμα. Κάποια στιγμή η ράβδος αφήνεται από τη θέση αυτή   και αρχίζει να γλιστράει μέσα στον κύλινδρο με τα άκρα της διαρκώς σε επαφή με τα εσωτερικά τοιχώματά του.

Θεωρείστε ότι κατά την πτώση της η ράβδος βρίσκεται διαρκώς στο ίδιο κατακόρυφο επίπεδο και    ότι η κίνησή της είναι καθαρά στροφική γύρω από τον άξονα του κυλίνδρου που διέρχεται από το O.

Υπολογίσετε τη γωνιακή ταχύτητα της ράβδου τη στιγμή που γίνεται οριζόντια.

Δίνεται για  τη ράβδο η ροπή αδράνειας Ι_c.m = (1/12)ML²_.

Θεωρείστε, για ευκολία, ότι g = 86/9 m/s².

Απ.  2r/s
Λύση σε pdf:  

Λύση σε word:

Μεταβάλλει η σανίδα την απόσταση ανάμεσα στους δυο κυλίνδρους;

Στο σχήμα η σανίδα που στηρίζεται στους δύο κυλίνδρους είναι οριζόντια. Τραβάμε τη σανίδα προς τα δεξιά έτσι ώστε το κέντρο του μικρότερου κυλίνδρου να κινείται με σταθερή ταχύτητα v. Η τριβή είναι αρκετά μεγάλη ώστε να αποτρέπει την ολίσθηση σε όλες τις επιφάνειες. Να βρείτε:

α) Αν οι δύο κύλινδροι θα πλησιάσουν ο ένας τον άλλον, θα απομακρυνθούν ή θα διατηρήσουν σταθερή τη μεταξύ τους απόσταση.

β) Το λόγο των επιταχύνσεων των σημείων επαφής των δύο κυλίνδρων με τη σανίδα.

γ) Αν η σανίδα μετατοπιστεί κατά 2πR πόσες περιστροφές θα έχει κάνει κάθε κύλινδρος;

Απάντηση σε pdf:  

Απάντηση σε word: