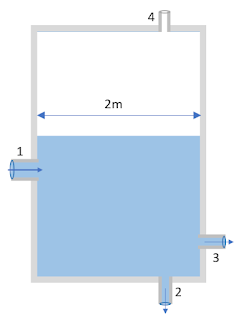
Η κλειστή δεξαμενή του σχήματος έχει ύψος Η = 2m
και περιέχει νερό μέχρι το ύψος h = 1,4 m και από εκεί και πάνω αέρα. Τα εμβαδά των καθέτων
τομών των σωλήνων στα σημεία Α και Ο είναι αντίστοιχα SA = 8 cm2 και So = 2 cm2.
H πίεση του αέρα μέσα στο δοχείο
είναι Ρ = 1,5·10 N/m2 και η πυκνότητα του νερού ρ = 103 kg/m3.
α) Να βρεθεί η ταχύτητα εκροής του νερού από το άνοιγμα στο Ο.
β) Να βρεθεί το ύψος h1 του νερού
στον ανοιχτό κατακόρυφο σωλήνα
ΑΒ.
(Θεωρείστε αμελητέο το εμβαδό της διατομής στο Ο σε σχέση με το
εμβαδό της επιφάνειας του υγρού στο κλειστό δοχείο).
γ) Σιγά – σιγά η στάθμη του νερού
στη δεξαμενή κατέρχεται και μετά πάροδο αρκετού χρόνου σταθεροποιείται σε ένα
ύψος h2. Να το
υπολογίσετε.
δ) Να βρείτε την τελική τιμή της πίεσης του αέρα μέσα στο δοχείο.
Δίνεται ότι: Patm = 105Ν/m2 και g
= 10 m/s2 και ότι η θερμοκρασία διατηρείται σταθερή.
ΟΔΗΓΙΑ Στα ρευστά, ό,που
έχω πιέσεις ή και ύψη εφαρμόζω νόμο Bernoulli, ό,που έχω διατομές εφαρμόζω νόμο συνέχειας. Σε σωλήνα με
στάσιμο υγρό εφαρμόζω τη σχέση της υδροστατικής. Αν ένα αέριο εκτονώνεται με σταθερή
θερμοκρασία τότε ισχύει PV σταθ.