ΜΙΑ, ΔΥΟ … ΠΟΛΛΕΣ ΚΡΟΥΣΕΙΣ!

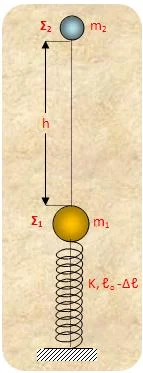
Ένα ελατήριο σταθεράς Κ = 75π² Ν/m είναι κατακόρυφο με το κάτω άκρο του σταθερά στερεωμένο σε οριζόντιο δάπεδο. Στο πάνω άκρο του ελατηρίου ισορροπεί,  στερεωμένη  σ΄ αυτό,  μια ελαστική σφαίρα  Σ₁ μάζας m₁ = 3 Kgr. Μια άλλη ελαστική σφαίρα Σ₂ μάζας m₂, συγκρατείται στην προέκταση του κατακόρυφου άξονα του ελατηρίου σε ύψος h = 5 m πάνω από τη Σ₁, όπως φαίνεται στο σχήμα. Κάποια στιγμή αφήνουμε τη σφαίρα Σ₂ ελεύθερη. Προσκρούει στη Σ₁ και αναπηδά σε ύψος h΄= h/4 πάνω από τη θέση που συνάντησε τη Σ₁. Αν η κρούση είναι μετωπική κι ελαστική, να υπολογίσετε:

   α) Τη μάζα m₂ της σφαίρας Σ₂.

   β) Πόσο είναι το πλάτος και η περίοδος της α.α.τ  της Σ₁;

   γ)  Δείξτε ότι μετά από ένα δευτερόλεπτο οι δύο σφαίρες θα συναντηθούν ξανά στη θέση όπου συγκρούστηκαν για πρώτη φορά, έχοντας, τη στιγμή της συνάντησης, αντίθετες ταχύτητες. 

   δ) Υπολογίστε τις ...

Κατεβάστε από εδώ όλη την άσκηση και από εδώ την απάντηση.

1 + 1 DOPPLER … ΜΕ ΠΑΡΕΛΘΟΝ

1. Περιπολικό αυτοκίνητο, του οποίου η σειρήνα παράγει ήχο συχνότητας 2900Hz, καταδιώκει μοτοσυκλετιστή . Η κίνηση και των δύο είναι ευθύγραμμη ομαλή. Όταν το περιπολικό και ο μοτοσυκλετιστής απέχουν 200 μέτρα, ο μοτοσυκλετιστής διαπιστώνει ότι ο ήχος της σειρήνας έχει συχνότητα 3100 Hz. Αν μετά από 10 sec το περιπολικό φτάσει το μοτοσυκλετιστή, να βρεθούν:

α) Oι ταχύτητες των δύο οχημάτων.

β) Η συχνότητα του ήχου που θα ακούει ο μοτοσυκλετιστής αν μετά το προσπέρασμα σταματήσει, ενώ το περιπολικό εξακολουθεί να κινείται προς την ίδια κατεύθυνση και με την ίδια ταχύτητα. ( Δίνεται η ταχύτητα του ήχου στον αέρα ίση με 340 m/sec)  (Πανελλήνιες εξετάσεις 1980). 

2. Σε ένα σημείο ευθύγραμμης σιδηροδρομικής γραμμής βρίσκεται ακίνητος παρατηρητής. Μια υπερταχεία πλησιάζει ...

Εδώ, μπορείτε να ... επαναφέρετε και τα δύο θέματα Doppler από το παρελθόν στο παρόν, με αναλυτική απάντηση σε μορφή pdf και εδώ να κατεβάσετε σε εικόνα jpeg το σπάνιο αυτό, δια χειρός εμού του ιδίου, πολυγραφημένο αντίγραφο, όπως διανεμήθηκε στους διαγωνιζόμενους της Γ Λυκείου στις Πανελλήνιες του 1980.

Πού είστε 49ρηδες!.

ΦΑΙΝΟΜΕΝΟ DOPPLER ΕΠΤΑ ΑΣΚΗΣΕΙΣ ΜΕ ΤΙΣ ΛΥΣΕΙΣ ΤΟΥΣ

Εξετάστε την ορθότητα της πρότασης: “όταν οι ταχύτητες παρατηρητή και πηγής παραγωγής ήχου είναι  ίδιες τότε ο παρατηρητής ακούει ήχο της ίδιας συχνότητας με αυτόν που εκπέμπει η πηγή, όμως το μήκος κύματος αυτού του ήχου είναι διαφορετικό από το πραγματικό”.

Όλες οι ερωτήσεις, με αναλυτικές απαντήσεις, βρίσκονται εδώ.

ΦΑΙΝΟΜΕΝΟ DOPPLER - ΘΕΜΑ Α "ΕΠΤΑ ΕΡΩΤΗΣΕΙΣ”

1.  Πότε ακούει μεγαλύτερη συχνότητα ένας παρατηρητής; Όταν απομακρύνεται με ταχύτητα υ από μία ακίνητη ηχητική πηγή ή όταν η ίδια ηχητική πηγή απομακρύνεται από τον ακίνητο παρατηρητή με ίδιου μέτρου ταχύτητα;

Οι υπόλοιπες ερωτήσεις και οι απαντήσεις εδώ.

ΚΡΟΥΣΕΙΣ – ΘΕΜΑ B “ΕΞΙ ΕΡΩΤΗΣΕΙΣ”

1.  Στην αριστερή στήλη του σχήματος φαίνονται δύο σφαίρες Α και Β αμέσως πριν συγκρουστούν, ενώ στη δεξιά έχουν σχεδιαστεί τρείς περιπτώσεις (1), (2) και (3) για την κατάστασή τους αμέσως μετά την κρούση.

Ποια από αυτές τις περιπτώσεις αντιστοιχεί σε:

i) αδύνατη κατάσταση,

ii) ελαστική κρούση,

iii) ανελαστική κρούση.

Αιτιολογείστε την επιλογή σας.

Η κρούση θεωρείται κεντρική και οι σφαίρες ολισθαίνουν χωρίς να κυλίονται.

Οι υπόλοιπες ερωτήσεις και οι απαντήσεις εδώ.

ΚΡΟΥΣΕΙΣ – ΘΕΜΑ Α “ΕΞΙ ΕΡΩΤΗΣΕΙΣ”

Δύο σφαίρες κινούνται κατά μήκος μιας ευθείας με αντίθετες ορμές και συ­γκρούονται πλαστικά. Άρα:

α. Μετά την κρούση οι δύο σφαίρες θα έχουν αντίθετες ορμές.

β. Η ολική κινητική ενέργεια του συστήματος μηδενίζεται.

γ. Πριν από την κρούση μεγαλύτερη κινητική ενέργεια είχε η σφαίρα με τη μεγαλύτερη μάζα.

δ. Περισσότερο μεταβλήθηκε το μέτρο της ορμής της σφαίρας με τη μεγαλύ­τερη μάζα.

ε. Η σφαίρα με τη μικρότερη μάζα θα χάσει, κατά την κρούση, περισσότερη κινητική ενέργεια.

Να χαρακτηρίσετε καθεμιά από τις παραπάνω προτάσεις ως σωστή ή λάθος.

Οι υπόλοιπες ερωτήσεις με τις απαντήσεις εδώ.

ΤΑ ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 2000 - 2014

ΗΜΕΡΗΣΙΑ		ΕΣΠΕΡΙΝΑ		ΕΛΛ. ΕΞΩΤΕΡΙΚΟΥ
ΚΑΝΟΝΙΚΕΣ	ΕΠΑΝΑΛΗΠΤΙΚΕΣ	ΚΑΝΟΝΙΚΕΣ	ΕΠΑΝΑΛΗΠΤΙΚΕΣ	ΚΑΝΟΝΙΚΕΣ
2000	2000	2000	2000	2000
2001	2001	2001	2001	2001
2002	2002	2002	2002	2002
2003	2003	2003	2003	2003
2004	2004	2004	2004	2004
2005	2005	2005	2005	2005
2006	2006	2006	2006	2006
2007	2007	2007	2007	2007
2008	2008	2008	2008	2008
2009	2009	2009	2009	2009
2010	2010	2010	2010	2010
2011	2011	2011	2011	2011
2012	2012	2012	2012	2012
2013	2013	2013	2013	2013
2014	2014	2014	2014	2014