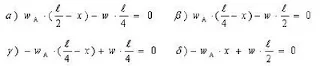ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ - ΘΕΜΑ Α

Η σανίδα του σχήματος είναι ομογενής, έχει μήκος ℓ και βάρος w και ισορροπεί σε ορι­ζόντια θέση με τη βοήθεια δύο υποστηριγ­μάτων, τα οποία απέχουν από κάθε άκρο της ℓ/4. Ένας άνθρωπος με βάρος w_A κινείται πάνω στη σανίδα από τη θέση του ενός υποστηρίγματος προς το πλησιέστερο άκρο της. Παρατηρούμε ότι η σανίδα αρχίζει να ανατρέπεται όταν ο άνθρωπος απέχει απόσταση x από το άκρο της. Ποια από τις παρακάτω σχέσεις ισχύει τη στιγμή ακριβώς της ανατροπής;

Δείτε εδώ όλες τις ερωτήσεις και εδώ τις αναλυτικές απαντήσεις.

ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2022

Δείτε εδώ τα θέματα του "ΠΑΝΕΛΛΗΝΙΟΥ ΔΙΑΓΩΝΙΣΜΟΥ ΦΥΣΚΗΣ"  2023 μαζί με τις λύσεις τους, καθώς  και των παλαιοτέρων ετών 2001 - 2022.

ΡΟΠΗ ΔΥΝΑΜΗΣ – ΘΕΜΑ Β, οι απαντήσεις.

Δείτε εδώ αναλυτικά τις απαντήσεις στο

ΡΟΠΗ ΔΥΝΑΜΗΣ – ΘΕΜΑ Β.

ΡΟΠΗ ΔΥΝΑΜΗΣ – ΘΕΜΑ Β

Στο καρούλι του σχήματος, το σχοινί είναι τυλιγμένο έτσι ώστε η δύναμη F να ασκείται, μέσω αυτού, στο κάτω μέρος του κυλίνδρου. 

Παρατηρούμε ότι όταν είναι F = 10N, οι τροχοί ολισθαίνουν χωρίς να περιστρέφονται. Η ακτίνα του κυλίνδρου και των τροχών είναι, αντίστοιχα, R₁ = 0,1m και R₂ = 0, 2 m,  ενώ η μάζα του συστήματος είναι m = 3 kgr. 

α) Να υπολογίσετε την τριβή ολισθήσεως μεταξύ κάθε τροχού και του δαπέδου.

β) Να υπολογίσετε την επιτάχυνση του κέντρου μάζας του καρουλιού.

Μπορείτε να δείτε όλες οι ερωτήσεις εδώ. 

ΡΟΠΗ ΔΥΝΑΜΗΣ - ΘΕΜΑ A

Σε ένα σημείο Α ενός επιπέδου σχήματος ενεργούν δύο δυνάμεις κάθετες  μεταξύ τους, που βρίσκονται πάνω σ’ αυτό το επίπεδο. Κάθετος στο επίπεδο και σε απόσταση d από την F₂ υπάρχει ένας άξονας zz΄ γύρω από τον οποίο το επίπεδο μπορεί να περιστρέφεται. Ο άξονας διέρχεται από ένα σημείο Ο που βρίσκεται πάνω στο φορέα της F₁. Μια τρίτη δύναμη, η F₃, εφαρμόζεται στο ίδιο σημείο Α και είναι παράλληλη στον άξονα zz΄. 

Aν F_1, = F₂ = F₃ = F, τότε τα μέτρα των ροπών των δυνάμεων αυτών ως προς τον άξονα zz΄ είναι, αντίστοιχα:  

α) 0, Fd, 0,     β)  0,  0, Fd,     γ) 0,  Fd,  Fd,        δ) Fd,  Fd,  Fd

Δείτε όλες τις ερωτήσεις εδώ.

ΚΥΛΙΣΗ ΧΩΡΙΣ ΟΛΙΣΘΗΣΗ - ΘΕΜΑ B . Οι απαντήσεις

Δείτε εδώ τις απαντήσες στο:
ΚΥΛΙΣΗ ΧΩΡΙΣ ΟΛΙΣΘΗΣΗ-ΘΕΜΑ B

ΚΥΛΙΣΗ ΧΩΡΙΣ ΟΛΙΣΘΗΣΗ – ΘΕΜΑ Β

Μια ομογενής τροχαλία ακτίνας R έχει άξονα ακτίνας r, (r < R), πάνω στον οποίο είναι τυλιγμένο λεπτό νήμα. Τραβάμε το νήμα με σταθερή ταχύτητα υ οριζόντια προς τα δεξιά, έτσι ώστε η τροχαλία να κυλίεται χωρίς να ολισθαίνει. Τότε το κέντρο μάζας θα κινηθεί με ταχύτητα:

Να αιτιολογήσετε την απάντησή σας.

Η συνέχεια εδώ: