Αρχική θέση = ακραία θέση (3ο μέρος)
Στις τέσσερις περιπτώσεις, που φαίνονται στα παρακάτω σχήματα, οι τιμές των μεγεθών έχουν επιλεγεί έτσι ώστε να μπορείτε να ακολουθήσετε με ευκολία τα βήματα που αναφέρονται στην απάντηση της προηγούμενης ανάρτησης. Σε κάθε περίπτωση αναφέρεται και η τελική απάντηση για να ελέγξετε την εργασία σας.
Εκφώνηση (κοινή για όλες τις περιπτώσεις).
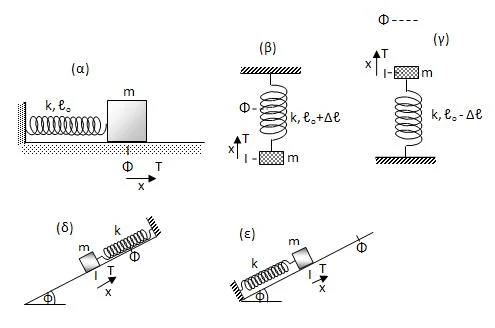
To σώμα, σε κάθε σχήμα, είναι προσδεμένο στο ένα άκρο ενός κατακόρυφου ελατηρίου. Αρχικά, με τη βοήθεια ενός σχοινιού ισορροπεί στη θέση Α. Τριβές δεν υπάρχουν.
α) Κάποια στιγμή κόβουμε το σχοινί. Nα δείξετε ότι το σώμα θα κάνει α.α.τ και ότι θα περνά περιοδικά από τη θέση Φ όπου το ελατήριο έχει το φυσικό του μήκος.
β) Βρείτε τον ελάχιστο χρόνο μεταξύ δύο διαδοχικών διελεύσεων του σώματος από τη θέση Φ.
α) Κάποια στιγμή κόβουμε το σχοινί. Nα δείξετε ότι το σώμα θα κάνει α.α.τ και ότι θα περνά περιοδικά από τη θέση Φ όπου το ελατήριο έχει το φυσικό του μήκος.
β) Βρείτε τον ελάχιστο χρόνο μεταξύ δύο διαδοχικών διελεύσεων του σώματος από τη θέση Φ.