Ένα καροτσάκι με τροχό και κύλινδρο

[Αλλιώς συμπεριφέρεται ο τροχός που ο άξονάς του είναι σταθερός ως προς το καρότσι και αλλιώς ο κύλινδρος που ο άξονας περιστροφής του είναι ελεύθερος].

Ένα καροτσάκι  Κ υποστηρίζεται από ένα τροχό Α και ένα κύλινδρο Β και οι δύο με ακτίνα 0,05 m. Αν κάποια στιγμή το καρότσι έχει επιτάχυνση 2,8 m/s² και ταχύτητα 1,6 m/s, με κατεύθυνση προς τα δεξιά, να βρείτε:

α. Τις γωνιακές ταχύτητες και επιταχύνσεις του τροχού Α και του κυλίνδρου Β.

β. Τις επιταχύνσεις των κέντρων του τροχού και του κυλίνδρου.

Ο κύλινδρος κυλίεται χωρίς να ολισθαίνει στην πλατφόρμα του καροτσιού και στο οδόστρωμα.

Απάντηση σε pdf: 
Απάντηση σε word:

Κύλινδρος σε ταλαντευόμενη πλατφόρμα

Ένας συμπαγής ομογενής κύλινδρος μάζας Μ και ακτίνας R είναι τοποθετημένος πάνω σε μια οριζόντια ορθογώνια πλατφόρμα μεγάλου μήκους. Αρχικά τα δυο σώματα είναι ακίνητα ως προς το έδαφος. Τη στιγμή  t = 0 η πλατφόρμα ξεκινά να εκτελεί ταλάντωση κατά τη διεύθυνση του άξονα xx΄ με εξίσωση x = x₀συνωt, όπου x η απομάκρυνση ενός σημείου της, έστω του Κ, από τη θέση ισορροπίας του (Ι). Ο κύλινδρος, με τον άξονά του ελεύθερο, σταθερά προσανατολισμένο κατά τη διεύθυνση του άξονα yy΄, κάθετη στη διεύθυνση της ταλάντωσης, αρχίζει να κυλίεται πάνω στην πλατφόρμα χωρίς να γλιστράει.  

Η μέγιστη ροπή που επενεργεί στον κύλινδρο κατά τη διάρκεια της κίνησης είναι:

α.	Μx0ω2R
	3

β.	Μx0ω2R
	2

γ.	2Μx0ω2R
	3

Να αποδείξετε την επιλογή σας.

Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονά του Ι_c = mR² / 2.

[Η άσκηση είναι παραλλαγή της άσκησης 40 σελ.387 σε μια προεπισκόπηση του βιβλίου ΙΤΤ Physics – 1]

Συμβουλή:  Η επιτάχυνση των σημείων της ακμής του κυλίνδρου που εφάπτεται της πλατφόρμας είναι ίση με την επιτάχυνση της πλατφόρμας. Μπορεί να μην έχουμε ολίσθηση, αλλά αν προσέξετε θα δείτε ότι εδώ δεν ισχύει η σχέση α_c = α_γR.

Απάντηση σε pdf: 
Απάντηση σε word:

Κύλινδρος σε σανίδα που επιταχύνεται

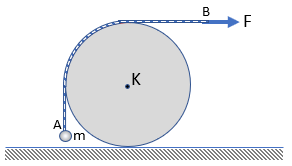
Μια επίπεδη σανίδα μάζας m = 1 kg ολισθαίνει πάνω σε μια λεία οριζόντια επιφάνεια με την επίδραση σταθερής οριζόντιας δύναμης F= 50 N. Πάνω της είναι τοποθετημένος ένας κύλινδρος μάζας  M = 2 kg και ακτίνας R = 1 m, όπως φαίνεται στο σχήμα. Αν ο κύλινδρος δεν γλιστράει πάνω στην επιφάνεια της σανίδας, να βρείτε:
α.  Τη γραμμική και τη γωνιακή επιτάχυνση του κυλίνδρου
β. Την επιτάχυνση της σανίδας και την τριβή της με τον κύλινδρο.

Δίνεται για τον κύλινδρο Ι_c = (1/2)ΜR². 

Πηγή: https://schools.aglasem.com/58655

Απάντηση σε pdf: 

Απάντηση σε word:


-----------------------------------------------------------------------------------------------------------------------

[Μετά από την παραπάνω θα σας φανούν πολύ απλές οι δύο παρακάτω παραλλαγές]:

1. Ένας ομογενής συμπαγής κύλινδρος μάζας Μ και ακτίνας R βρίσκεται πάνω σε μια οριζόντια πλατφόρμα που κινείται με σταθερή επιτάχυνση α_π = 3 m/s². Αν ο κύλινδρος κυλά χωρίς να γλιστράει πάνω στην πλατφόρμα με τον άξονά του κάθετο στη διεύθυνση κίνησης της πλατφόρμας,

α. Προσδιορίστε το μέγεθος της επιτάχυνσης του κέντρου μάζας του κυλίνδρου.

β. Αν ο μέγιστος συντελεστής στατικής τριβής είναι ίσος με τον συντελεστή τριβής ολισθήσεως μ_ολ = 0,4, να βρείτε τη μέγιστη επιτάχυνση που μπορεί να έχει η πλατφόρμα χωρίς ολίσθηση μεταξύ του κυλίνδρου και πλατφόρμας.

Απάντηση 

----------------------------------------------------------------------------------------------------------------------

2.

Ένα κέρμα μάζας m και ακτίνας R στέκεται κάθετα στο δεξιό άκρο μιας οριζόντιας σανίδας μάζας Μ και μήκους L = 1 m, όπως φαίνεται στο σχήμα. Το σύστημα αρχικά ηρεμεί ως προς το έδαφος. Στη συνέχεια, τη χρονική στιγμή t = 0, η σανίδα τραβιέται προς τα δεξιά με μια σταθερή δύναμη και αρχίζει να κινείται με σταθερή επιτάχυνση α_σ = 3 m/s². Αν το νόμισμα δεν γλιστρά σε σχέση με τη σανίδα,

 α) Με πόση επιτάχυνση θα κινηθεί το κέρμα;

β) Πόσο μακριά προς τα δεξιά το κέρμα κινείται μέχρι να φτάσει το αριστερό άκρο της σανίδας;

β) Ποια χρονική στιγμή το νόμισμα θα φτάσει στο άλλο άκρο της σανίδας;

Δίνεται η ροπή αδράνειας Ι_c = MR²/2, για το κέρμα.

Απάντηση:

Ομαλή κύλιση κυλίνδρου σε κινούμενη με σταθερή ταχύτητα σανίδα

Το πλαίσιο αναφοράς των ταχυτήτων είναι το έδαφος. Αν ο κύλινδρος κυλίεται χωρίς ολίσθηση πάνω στη σανίδα, η ταχύτητα του ανώτερου σημείου Α του τροχού είναι:

 α) 2V_Κ

β) 2V_Κ + V_σ

γ) 2V_Κ – V_σ

δ) (V_Κ-V_σ) 

Απάντηση σε pdf: 

Απάντηση σε word:

Κύλιση κυλίνδρου με σταθερή ταχύτητα σε σανίδα που στηρίζεται σε λείο δάπεδο

Ένας κύλινδρος εκτελεί κύλιση χωρίς ολίσθηση με σταθερή ταχύτητα v πάνω σε μια σανίδα, της οποίας η πάνω επιφάνεια είναι αρκετά τραχιά, αλλά η κάτω επιφάνεια είναι λεία. Αν κόψουμε το σχοινί που συγκρατεί τη σανίδα, τότε:

α) Η σανίδα θα κατευθυνθεί προς τα δεξιά.

β) Η σανίδα θα κατευθυνθεί προς τα αριστερά.

γ) Η σανίδα θα παραμείνει ακίνητη.

δ) Η κατεύθυνση προς την οποία θα κινηθεί η σανίδα εξαρτάται από το αν η μάζα της είναι μεγαλύτερη ή μικρότερη από τη μάζα του κυλίνδρου. 

Απάντηση σε pdf: 
Απάντηση σε word:

Κύλιση τροχού με σταθερή επιτάχυνση σε παράλληλες σιδηροτροχιές

Ένα αβαρές, μη εκτατό σχοινί, είναι περασμένο στο αυλάκι μιας αβαρούς τροχαλίας Π, που μπορεί να περιστρέφεται χωρίς τριβές γύρω από ακλόνητο οριζόντιο άξονα και στη συνέχεια είναι τυλιγμένο πολλές φορές στην περιφέρεια ενός ομογενούς τροχού T ακτίνας R, που μπορεί να περιστρέφεται μαζί με τον άξονά του, ο οποίος είναι ένας αβαρής κύλινδρος ακτίνας R/2 σταθερά συνδεμένος με αυτόν. Ο κυλινδρικός άξονας του τροχού, μπορεί να κυλήσει χωρίς ολίσθηση κατά μήκος δύο οριζόντιων παράλληλων σιδηροτροχιών P, (επειδή στο σχήμα α φαίνεται μόνο η σιδηρογραμμή στην μπροστινή όψη του τροχού, στο σχήμα β παρατίθεται σχετική κάτοψη). Η μάζα του τροχού είναι Μ και  η ροπή αδράνειάς του ως προς τον νοητό άξονα που είναι κάθετος στο κέντρο C του τροχού είναι (1/2)ΜR². Αν το άκρο Λ του σχοινιού τραβιέται προς τα κάτω με σταθερή επιτάχυνση g/2 και το σχοινί δεν ολισθαίνει καθώς ξετυλίγεται, να βρείτε:

α) Την κατεύθυνση προς την οποία θα κινηθεί το κέντρο C του τροχού.

β) Την επιτάχυνση του κέντρου C.

γ) Την κατεύθυνση και το μέτρο της τριβής μεταξύ της επιφάνειας του κυλινδρικού άξονα και των σιδηροτροχιών.

δ) Την τάση του σχοινιού.

Απάντηση σε pdf:  
Απάντηση σε word:

Πλαίσιο, μαγνητικό πεδίο, ρεύμα, σχοινιά και τάσεις

Ένας ομοιόμορφος (ομογενής και ισοπαχής) ορθογώνιος βρόχος με μήκη πλευρών d,ℓ (d < ℓ) και με μάζα m κρέμεται οριζόντια με τη βοήθεια δύο κατακόρυφων σχοινιών. Ο βρόχος διαρρέεται από ρεύμα i και βρίσκεται μέσα σε ένα ομογενές οριζόντιο μαγνητικό πεδίο Β το οποίο είναι παράλληλο με τη μακρύτερη πλευρά του.

H τάση του σχοινιού που είναι δεμένο στο σημείο Α είναι:

                             α) mg – Bid,    β) mg/2 – Bid,     γ) mg/2 +Bid

Να επιλέξετε με αιτιολόγηση την ορθή σχέση. 

Απάντηση σε pdf:  
Απάντηση σε word:

Επιτάχυνση του σημείου επαφής τροχού – κυρτής επιφάνειας

 Μια κυρτή επιφάνεια έχει ομοιόμορφη ακτίνα καμπυλότητας ίση με 6R. Ένας τροχός ακτίνας R κυλίεται χωρίς να ολισθαίνει πάνω της με ταχύτητα υ σταθερού μέτρου. Η επιτάχυνση των σημείων του τροχού ως προς το κέντρο Ο της κυρτής επιφάνειας, τη στιγμή που έρχονται σε επαφή με αυτήν, έχει μέτρο:

                                                    α) 6υ²/7R,     β) 5υ²/6R,     γ) μηδέν 

Απάντηση σε pdf: 
Απάντηση σε word:

Η προφανής και η «αφανής» στατική τριβή στη μη ολίσθηση

Στο σχήμα φαίνεται η εγκάρσια κατακόρυφη τομή ενός οριζόντιου ομογενούς κυλίνδρου, που το κέντρο της ταυτίζεται με το κέντρο μάζας του κυλίνδρου. Ένα μικρό σώμα μάζας m κρατιέται σε ισορροπία δεμένο στην άκρη Α ενός σχοινιού αμελητέας μάζας, του οποίου ένα τμήμα εφάπτεται στον κύλινδρο, όπως φαίνεται στο σχήμα. Η άλλη άκρη B του σχοινιού τραβιέται από μια οριζόντια δύναμη F. Αν το σχοινί δεν ολισθαίνει στην επιφάνεια του κυλίνδρου και ο κύλινδρος ηρεμεί στην οριζόντια επιφάνεια, το μέτρο της F είναι ίσο με:

                                       α)  mg/2            β) mg,             γ)  3mg/2

Σύντομη απάντηση: 
Αναλυτική απάντηση σε pdf: 
Αναλυτική απάντηση σε word:

Περιστροφή δίσκου γύρω από οριζόντια χορδή του

Ένας ομογενής κυκλικός δίσκος έχει ακτίνα R και μάζα m. Ένα σωματίδιο, επίσης μάζας m, είναι στερεωμένο στο σημείο Σ στην άκρη του δίσκου όπως φαίνεται στο σχήμα. Ο δίσκος μπορεί να περιστρέφεται χωρίς τριβές γύρω από τον σταθερό οριζόντιο άξονα ΡΡ΄, πάνω στον οποίο βρίσκεται η χορδή ΑΒ που απέχει R / 4 από το κέντρο Κ του δίσκου και είναι κάθετη στην προέκταση της ακτίνας ΣΚ. Αρχικά, ο δίσκος κρατείται κατακόρυφα με το σωματίδιο στο σημείο Σ στην υψηλότερη θέση του. Στη συνέχεια αφήνεται να πέσει, έτσι ώστε να αρχίσει να περιστρέφεται γύρω από τοnν άξονα PΡ΄. 

Βρείτε τη γραμμική ταχύτητα του σωματιδίου καθώς φθάνει στη χαμηλότερη θέση του.

Δίνεται ότι η ροπή αδράνειας ομογενούς κυκλικού δίσκου ως προς άξονα που βρίσκεται στο επίπεδό του και διέρχεται από το κέντρο του είναι I = mR²/4. 

Απάντηση σε pdf 
Απάντηση σε word:

Κατακόρυφη περιστροφή ράβδου στο εσωτερικό κοίλου κυλίνδρου

[Εδώ, μια ράβδος στρέφεται γύρω από άξονα που δεν διέρχεται από το φορέα της]

Θεωρείστε ένα κοίλο κύλινδρο σταθερό σε οριζόντιο επίπεδο, με λεία εσωτερική επιφάνεια ακτίνας     R = 5 m και μια ομογενή ράβδο μάζας M και μήκους L = 8 m, που συγκρατείται αρχικά σε κατακόρυφη θέση όπως φαίνεται στο σχήμα. Κάποια στιγμή η ράβδος αφήνεται από τη θέση αυτή   και αρχίζει να γλιστράει μέσα στον κύλινδρο με τα άκρα της διαρκώς σε επαφή με τα εσωτερικά τοιχώματά του.

Θεωρείστε ότι κατά την πτώση της η ράβδος βρίσκεται διαρκώς στο ίδιο κατακόρυφο επίπεδο και    ότι η κίνησή της είναι καθαρά στροφική γύρω από τον άξονα του κυλίνδρου που διέρχεται από το O.

Υπολογίσετε τη γωνιακή ταχύτητα της ράβδου τη στιγμή που γίνεται οριζόντια.

Δίνεται για  τη ράβδο η ροπή αδράνειας Ι_c.m = (1/12)ML²_.

Θεωρείστε, για ευκολία, ότι g = 86/9 m/s².

Απ.  2r/s
Λύση σε pdf:  

Λύση σε word:

Μεταβάλλει η σανίδα την απόσταση ανάμεσα στους δυο κυλίνδρους;

Στο σχήμα η σανίδα που στηρίζεται στους δύο κυλίνδρους είναι οριζόντια. Τραβάμε τη σανίδα προς τα δεξιά έτσι ώστε το κέντρο του μικρότερου κυλίνδρου να κινείται με σταθερή ταχύτητα v. Η τριβή είναι αρκετά μεγάλη ώστε να αποτρέπει την ολίσθηση σε όλες τις επιφάνειες. Να βρείτε:

α) Αν οι δύο κύλινδροι θα πλησιάσουν ο ένας τον άλλον, θα απομακρυνθούν ή θα διατηρήσουν σταθερή τη μεταξύ τους απόσταση.

β) Το λόγο των επιταχύνσεων των σημείων επαφής των δύο κυλίνδρων με τη σανίδα.

γ) Αν η σανίδα μετατοπιστεί κατά 2πR πόσες περιστροφές θα έχει κάνει κάθε κύλινδρος;

Απάντηση σε pdf:  

Απάντηση σε word:

Είναι δυνατό δύο ομογενείς σφαίρες σε επαφή να ισορροπούν μόνες τους πάνω σε πλάγιο επίπεδο;

[Μια ομογενής σφαίρα μόνη της, προφανώς, δεν μπορεί να ισορροπήσει σε πλάγιο επίπεδο. Δύο όμως;]

Δύο ομογενείς σφαίρες Α και Β έχουν τοποθετηθεί πάνω σε ένα πλάγιο επίπεδο έτσι ώστε να εφάπτονται μεταξύ τους. Παρατηρούμε ότι παραμένουν σε ισορροπία. Οι ακτίνες των δύο σφαιρών είναι ίσες. Ποια σφαίρα έχει μεγαλύτερη μάζα; 

Απάντηση σε pdf:  
Απάντηση σε word:

Ισορροπία τροχού με ενσωματωμένο ταλαντωτή

[Ο σημαντικός ρόλος της δύναμης  του ελατηρίου στο σημείο στήριξής του.]

Ένας τροχός μπορεί να περιστρέφεται ελεύθερα σε κατακόρυφο επίπεδο, γύρω από ακλόνητο κεντρικό οριζόντιο άξονα, χωρίς τριβή.

Υπάρχει μια οριζόντια ελαφριά ράβδος στερεωμένη στον τροχό κάτω από τον άξονα σε απόσταση d από αυτόν και ένα μικρός δακτύλιος μάζας m που μπορεί να ολισθαίνει κατά μήκος της ράβδου χωρίς τριβή. Ο δακτύλιος συνδέεται με ένα ελαφρύ ελατήριο. Το άλλο άκρο του ελατηρίου στερεώνεται στο χείλος του τροχού, όπως φαίνεται στο σχήμα. Αρχικά ο δακτύλιος  ισορροπεί στο κέντρο της ράβδου και το ελατήριο έχει το φυσικό του μήκος. Κρατάμε τον τροχό ώστε η ράβδος να παραμείνει οριζόντια, μετακινούμε προς τα δεξιά τον δακτύλιο και το ελατήριο συμπιέζεται.

Κάποια στιγμή ελευθερώνουμε ταυτόχρονα τον τροχό και τον δακτύλιο.  

α) Είναι δυνατόν ο τροχός να μην περιστρέφεται καθώς ο δακτύλιος εκτελεί α.α.τ. στη ράβδο;

β) Βρείτε την τιμή της σταθεράς ελατηρίου k ώστε η κατάσταση που περιγράφεται στο (α) να είναι δυνατή. 

Απάντηση σε pdf: 

Τροχαλία και κουβάς

[Εφαρμογή της Α.Δ.Ε όταν ο κουβάς αφήνεται ελεύθερος να κατέβει.]

Χρησιμοποιήστε την αρχή διατήρησης της ενέργειας  για να υπολογίσετε τη γωνιακή ταχύτητα της τροχαλίας που φαίνεται στο σχήμα, τη στιγμή που ο κάδος μάζας m = 3 kg έχει κατέλθει κατά h = 3 m, ξεκινώντας από την ηρεμία. Θεωρείστε αμελητέα τη μάζα του σχοινιού που είναι προσαρτημένο στον κάδο και τυλιγμένο πολλές φορές γύρω από την τροχαλία και ότι δεν γλιστρά καθώς ξετυλίγεται.

Η τροχαλία περιστρέφεται χωρίς τριβές.

Δίνεται η μάζα Μ = 4 kg, η ακτίνα R = 0,6 m και η ροπή αδράνειας I = MR²/2 της  τροχαλίας καθώς και ότι η επιτάχυνση βαρύτητας ισούται με g = 10 m/s². 

Απάντηση:

Ένας ψύκτης νερού

Από ένα ψύκτη νερού εκτινάσσεται νερό σε ύψος h = 12 cm πάνω από ένα ακροφύσιο διαμέτρου D₂ =  0,60 cm. Η αντλία που βρίσκεται στη βάση της συσκευής (Η = 1,1 m κάτω από το ακροφύσιο) ωθεί το νερό σε σωλήνα τροφοδοσίας σταθερής διαμέτρου D₁ = 1,2 cm, που καταλήγει στο ακροφύσιο. 
α) Με πόση πίεση εισάγει η αντλία το νερό στο σωλήνα τροφοδοσίας; Δίνονται η επιτάχυνση βαρύτητας g = 10 m/s², η ατμοσφαιρική πίεση Ρ = 10⁵N/m² και η πυκνότητα του νερού ρ = 10³ kg/m³.

β) Μπορείτε με τα παραπάνω δεδομένα να υπολογίσετε την ισχύ της αντλίας του ψύκτη;
Αιτιολογείστε την απάντησή σας.
Να μη λάβετε υπόψη το ιξώδες του νερού και τις τριβές με τα τοιχώματα του σωλήνα.

Πηγή: PHYSICS

PRINCIPLES WITH APPLICATIONS

DOUGLAS C. GIANCOLI

              Απάντηση:

Ροή υγρού σε σωλήνα μεταβλητής διατομής και υψομετρική διαφορά

Νερό ρέει από τον οριζόντιο σωλήνα μεγαλύτερης διαμέτρου, ίσης με 20 cm, προς τον στενότερο σωλήνα διαμέτρου από 5 έως 10 cm. Το οριζόντιο τμήμα του στενότερου σωλήνα βρίσκεται 2 μέτρα υψηλότερα από τον φαρδύτερο, όπως στην εικόνα. Εάν το νερό ρέει στον μεγαλύτερο σωλήνα με ταχύτητα 4 m / s,

α) Με ποια ταχύτητα ρέει στον μικρότερο σωλήνα;

α) 2 m/s  

β) 8 m/s  

γ) 14m/s  

δ) 20  m/s

Επιλέξτε την επιτρεπτή τιμή της ζητούμενης ταχύτητας.

β) Αυξάνεται ή μειώνεται κατά την άνοδο του νερού ή στατική πίεση;

Φλέβα υγρού κυλινδρικής διατομής

[ Όπου τα μόρια ενός υγρού οδηγούνται ακτινικά προς ένα κέντρο απορροής– Ένα θέμα Β πρωτότυπο και απλό.]

Μια επίπεδη οριζόντια επιφάνεια έχει μια μικρή οπή στο κέντρο της. Μια κυκλική γυάλινη πλάκα ακτίνας R τοποθετείται συμμετρικά πάνω από την οπή με ένα μικρό διάκενο h να παραμένει μεταξύ της πλάκας και της επιφάνειας. Ένα υγρό εισέρχεται στο διάκενο συμμετρικά από όλες τις πλευρές και αφού ταξιδεύει ακτινικά διαμέσου του διακένου τελικά καταλήγει στην οπή απ’ όπου εξέρχεται. Η παροχή όγκου του υγρού που βγαίνει από την οπή είναι Π (σε m³/s).

α) Αν η ταχύτητα ροής ακριβώς κάτω από την περιφέρεια της κυκλικής πλάκας είναι υ₀,  να βρείτε  την ταχύτητα (V_x)  ροής μέσα στο διάκενο σε απόσταση x (βλέπε εικόνα) από το κέντρο της οπής.

β) Ποια σχέση συνδέει τη  V_x με τα μεγέθη Π, h και x;

Να θεωρήσετε τη ροή του υγρού προς την οπή, μόνιμη και στρωτή.

Απάντηση: