Αλληλεπίδραση ρευμάτων ευθύγραμμων αγωγών, 3ο

Τι θα συμβεί στον αγωγό ΓΔ του προηγουμένου προβλήματος αν διαβιβάσουμε σε αυτόν ρεύμα που έχει φορά από το άκρο Δ προς το Γ; 

Ένα από τα πειράματα που πραγματοποίησε ο Lenz για την επαλήθευση του περίφημου «κανόνα» του

Στο έργο του "Πώς να προσδιορίσετε την κατεύθυνση των επαγόμενων ρευμάτων", όπου ο διάσημος κανόνας του Lenz καθορίστηκε για πρώτη φορά, ο ακαδημαϊκός H.F.E. Lenz περιγράφει μερικά από τα πειράματα που πραγματοποίησε για να καθορίσει την κατεύθυνση των επαγόμενων ρευμάτων. Ένα από αυτά είναι η περίπτωση ενός επαγόμενου ρεύματος παραγόμενου σε έναν κυκλικό αγωγό Α όταν αυτός περιστρέφεται κατά 90° σε σχέση με έναν άλλο κυκλικό αγωγό Β ο οποίος διαρρέεται από ρεύμα. Καθορίστε την κατεύθυνση του επαγόμενου ρεύματος στον κυκλικό αγωγό Α αν περιστραφεί από μία θέση κάθετη στον αγωγό Β σε θέση παράλληλη προς αυτόν, όπως υποδεικνύεται από το βέλος.

Απάντηση:

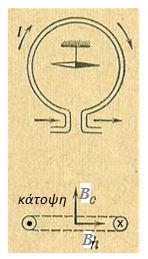
Πώς θα συμπεριφερθούν δύο κατακόρυφοι κυκλικοί αγωγοί

Δύο κατακόρυφοι κυκλικοί αγωγοί με περίπου ίσες διαμέτρους είναι τοποθετημένοι σε κάθετα μεταξύ τους επίπεδα όπως φαίνεται στο σχήμα.

α) Πώς θα συμπεριφερθούν οι αγωγοί εάν διαβιβάσουμε σε καθένα από αυτούς ρεύμα με φορά που υποδεικνύεται από τα βέλη; 

β) Ν απαντήσετε στο ίδιο ερώτημα αν το ένα από τα δύο ρεύματα, έστω το Ι2,  έχει αντίστροφη φορά από αυτήν του σχήματος.

Απάντηση:

Προσδιορισμός της κατεύθυνσης επαγόμενου ρεύματος

Ο νότιος πόλος ενός μαγνήτη απομακρύνεται με μια ορισμένη ταχύτητα από ένα μεταλλικό δακτύλιο όπως φαίνεται στο σχήμα. Προσδιορίστε την κατεύθυνση του επαγόμενου ρεύματος στο δακτύλιο. 

Απάντηση:

Πηνίο, ρεύμα και ακίνητος μαγνήτης

 Ένα πηνίο πολλών σπειρών από λεπτό σύρμα, διαρρέεται από ηλεκτρικό ρεύμα και κρέμεται όπως φαίνεται στο σχήμα. Ένας λεπτός οριζόντιος μαγνήτης έρχεται κοντά στο πηνίο.

Τι θα συμβεί στο πηνίο σε αυτή την περίπτωση αν η φορά του ρεύματος που διαρρέει τις σπείρες του είναι αυτή που φαίνεται στο σχήμα;

Απάντηση:

Με ποια δύναμη αλληλεπιδρούν τα ρεύματα ενός ευθύγραμμου κι ενός κυκλικού αγωγού;

Ένας ευθύγραμμος αγωγός διαρρέεται από ρεύμα έντασης I₂ και είναι τοποθετημένος κατά μήκος του άξονα ενός κυκλικού αγωγού που διαρρέεται από ρεύμα έντασης Ι₁ .

Με ποια δύναμη αλληλεπιδρούν τα ρεύματα; 

Απάντηση:

Ελάττωση του μήκους ενός μαλακού ελατηρίου εξαιτίας του Μ.Π του ρεύματος

Ένα μαλακό σπειροειδές ελατήριο κρέμεται ελεύθερα. Το κάτω άκρο του ελατηρίου βυθίζεται σε ένα κύπελλο με υδράργυρο. Το ελατήριο και το κύπελλο συνδέονται με μία πηγή συνεχούς ρεύματος όπως φαίνεται στο σχήμα.

Τι θα συμβεί στο ελατήριο μετά το κλείσιμο του κυκλώματος από έναν διακόπτη δ;

Απάντηση:

Μια μη μαγνητισμένη ράβδος σιδήρου εισέρχεται μέσα στο μαγνητικό πεδίο πηνίου

Μια μη μαγνητισμένη ράβδος σιδήρου αφήνεται από κάποιο ύψος να πέσει κινούμενη κατά μήκος της κατακορύφου που ταυτίζεται με τον άξονα ενός πηνίου με οριζόντιες σπείρες, συνδεδεμένου με μια ηλεκτρική μπαταρία και ένα αμπερόμετρο, όπως στο σχήμα. Σχεδιάστε κατά προσέγγιση ένα διάγραμμα i – t της έντασης του ρεύματος που διαρρέει το πηνίο με το χρόνο καθώς η ράβδος διέρχεται μέσα από αυτό. 

Απάντηση:

Η περίεργη συμπεριφορά ενός ελεύθερου ρευματοφόρου αγωγού πάνω από ένα μαγνήτη

Ένας ευθύγραμμος ρευματοφόρος αγωγός είναι τοποθετημένος πάνω από τους πόλους ενός πεταλοειδούς μαγνήτη όπως φαίνεται στο σχήμα. Ο αγωγός μπορεί να κινηθεί ελεύθερα προς όλες τις κατευθύνσεις.

Τι θα συμβεί στον αγωγό κάτω από τη δράση του πεδίου του μαγνήτη εάν το ρεύμα έχει την κατεύθυνση που δείχνει το βέλος; 

 Απάντηση:

Ρεύμα σε πηνίο και μαγνήτης με κοινό άξονα

Τι θα συμβεί στον μόνιμο ευθύγραμμο μαγνήτη αν τα άκρα του σωληνοειδούς συνδεθούν με τους πόλους μια πηγής όπως στο σχήμα;

Απάντηση: 

Μαγνήτες και πηνία σε σχετική κίνηση πάνω σε κοινό άξονα

Να σχεδιάσετε τη φορά του επαγόμενου ρεύματος

α) στο πηνίο και

β) στον κυκλικό αγωγό

Να αιτιολογήσετε σε κάθε περίπτωση τη φορά του ρεύματος που επιλέξατε. 

Απάντηση:

Προς τα πού θα περιστραφεί η μαγνητική βελόνα (1ο)

Σε ένα επίπεδο κυκλικό  δίσκο τοποθετούμε μια ποσότητα αρνητικού ηλεκτρικού φορτίου και στη συνέχεια τον θέτουμε σε ταχεία περιστροφή γύρω από οριζόντιο άξονα που έχει την κατεύθυνση ανατολής – δύσης. Το μαγνητικό πεδίο που δημιουργείται από το φορτίο στο δίσκο μπορούμε να το ανιχνεύσουμε με τη βοήθεια μίας μαγνητικής βελόνας  που τοποθετείται πάνω από το δίσκο όπως φαίνεται στο σχήμα.

 Η βελόνα αρχικά, πριν την περιστροφή του δίσκου, ισορροπεί  κατά τη διεύθυνση βορρά – νότου (υπό τη επίδραση του γήινου μαγνητικού πεδίου). Προσδιορίστε την κατεύθυνση προς την οποία εκτρέπεται η βελόνα αν ο δίσκος περιστρέφεται κατά τη φορά που φαίνεται στο σχήμα. 

Απάντηση:

Προς τα πού θα περιστραφεί η μαγνητική βελόνα (2ο)

Μερικές φορές τα ρεύματα μετρούνται με τη βοήθεια του λεγόμενου «εφαπτόμενου γαλβανόμετρου». Αυτό αποτελείται από μια μικρή μαγνητική βελόνα αιωρούμενη από ένα ελαφρύ νήμα που είναι τοποθετημένη στο κέντρο ενός κυκλικού αγωγού. Το επίπεδο του κυκλικού αγωγού είναι κατακόρυφο με προσανατολισμό βορρά - νότου. Έτσι αρχικά ο άξονας της μαγνητικής βελόνας ταυτίζεται με την οριζόντια διάμετρο του κυκλικού αγωγού. Προσδιορίστε τη γωνία κατά την οποία θα περιστραφεί και θα ισορροπήσει η μαγνητική βελόνα του γαλβανόμετρου αν περάσει ένα ρεύμα I = 10 A κατά μήκος του κυκλικού αγωγού. Δίνεται η ακτίνα του κυκλικού αγωγού R = 10 cm και η οριζόντια συνιστώσα του γήινου μαγνητικού πεδίου Β_h = 2π· 10^-5 T,  k_μ­= 10^-7 . Δίνεται k_μ = 10^-7 Ν/Α². 

Απάντηση:

Προς τα πού θα περιστραφεί η μαγνητική βελόνα (3ο)

 Ένα ρεύμα Ι διαβιβάζεται κατά μήκος του δακτυλίου του εφαπτόμενου γαλβανόμετρου στο προηγούμενο πρόβλημα, το οποίο δημιουργεί ένα πεδίο έντασης 10^-5 Τesla στο κέντρο του δακτυλίου. Περιστρέφουμε σιγά – σιγά τον δακτύλιο και παρατηρούμε ότι το ίδιο κάνει και η μαγνητική βελόνα. Προσδιορίστε τη γωνία κατά την οποία πρέπει να περιστραφεί ο δακτύλιος έτσι ώστε η βελόνα να ισορροπήσει  στο επίπεδο αυτού του δακτυλίου. 

Απάντηση:

Προς τα πού θα περιστραφεί η μαγνητική βελόνα (4ο)

Το σχήμα απεικονίζει έναν αγωγό με μια μαγνητική βελόνα που αρχικά ισορροπεί παράλληλα προς αυτόν ακριβώς από κάτω. Κάποια στιγμή διαβιβάζουμε ρεύμα στον αγωγό.

Α. Ποια θα είναι η κατεύθυνση του ρεύματος αν ο νότιος πόλος της βελόνας εκτραπεί προς τον αναγνώστη;

Β. Τι θα συμβεί στην εκτροπή της βελόνας, εάν η τελευταία τοποθετηθεί πάνω στον αγωγό; 

Απάντηση:

Ρεύμα και μαγνητικό πεδίο σε ευθύγραμμους και πεταλοειδείς ηλεκτρομαγνήτες

  Προσδιορίστε την πολικότητα των ηλεκτρομαγνητών στο σχήμα (α) και τη φορά του ρεύματος στα σύρματα του σχήματος (β).

(Προσέξτε την περιέλιξη στους δύο βραχίονες του πεταλοειδούς ηλεκτρομαγνήτη)

Απάντηση:

Θέματα και απαντήσεις επαναληπτικών Πανελλαδικών εξετάσεων στη Φυσική 2019

Δείτε τα θέματα:

των Ημερησίων και Εσπερινών (κοινά θέματα) εδώ

και τα θέματα Ομογενών εδώ  

Σχόλια και απαντήσεις εδώ

Πανελλήνιες στη Φυσική, 2019 τα Θέματα και οι Λύσεις τους

Τα Θέματα των Ημερησίων

Τα Θέματα των Εσπερινών

(Στο Β1 δόθηκε η διευκρίνση ότι το δάπεδο είναι λείο και στο Β3 ότι το σώμα μάζας m είναι, αρχικά, ακίνητο).

Σύντομες Απαντήσεις

Οι Λύσεις (από το υλικονετ)

Σχόλια (συναδέλφων στο υλικονετ)

2ο Τρίωρο διαγώνισμα σε όλη την ύλη

Η εκφώνηση 

Οι απαντήσεις

3ωρο ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΡΕΥΣΤΑ

Το Διαγώνισμα

                                                                  Οι Απαντήσεις

Το 1ο γενικό διαγώνισμα στα κύματα πλήρως αναθεωρημένο και βελτιωμένο

ΘΕΜΑ Α

 (Σημειώστε το σωστό συμπλήρωμα καθεμιάς  από τις παρακάτω ημιτελείς προτάσεις )

 A.1. Μια πηγή απλού ήχου συχνότητας 600 Hz είναι τοποθετημένη σε κάποιο βάθος μέσα σε μια λίμνη νερού. Η ταχύτητα του ήχου στο νερό είναι 1500 m/s ενώ  στον αέρα είναι 300 m/s. Η συχνότητα του ήχου που καταγράφεται από μια  συσκευή που βρίσκεται έξω από τη λίμνη είναι:

      α. 3000 Ηz,                 β. 200 Ηz,                 γ. 600 Ηz,                   δ. 120 Ηz

Α.2.  Μηχανικό αρμονικό κύμα που διαδίδεται σε γραμμικό ελαστικό μέσο μεγάλου μήκους περιγράφεται από την εξίσωση:

                                             ψ = 0,1ημ4π(50t – x),  (S.I)

Τη χρονική στιγμή t₁ = 0,2sec το κύμα έχει διαδοθεί σε απόσταση:

     α. 10m,                    β. 1m,                     γ. 0,5m,                    δ. 100m

Α.3.  Δύο σύγχρονες πηγές κυμάτων βρίσκονται στα σημεία Α και Β της επιφάνειας μιας   λίμνης και παράγουν υδάτινα αρμονικά κύματα. Η καθεμιά παράγει κύμα μήκους κύματος 2 m. Μια πάπια, που βρίσκεται στο μέσον Μ του ευθυγράμμου τμήματος ΑΒ, ενοχλείται  από το αποτέλεσμα της συμβολής των κυμάτων και επιζητεί να πάει σε θέση όπου δε θα ταλαντώνεται. Η ελάχιστη απόσταση που πρέπει να διανύσει ώστε να βρεθεί σε μια τέτοια θέση είναι

  α. 0,25 m,               β. 0,50 m,                γ. 0,75 m,              δ. 1 m          

Α.4. Κατά μήκος μιας χορδής έχει δημιουργηθεί στάσιμο κύμα, που περιγράφεται από την εξίσωση ψ = Dσυν(2πx/λ)·ημ2πt  (S.I). H απόσταση μεταξύ δύο διαδοχικών δεσμών του είναι α m. Αν η εξίσωση ταλάντωσης ενός σημείου Μ της χορδής, για το οποίο είναι x_Μ = ⅔α m, είναι ψ_Μ = 0,02ημ(2πt + π)  (S.I). Τότε:

α)  Το πλάτος των κοιλιών του είναι 0,02 m.

β)  Το πλάτος των κοιλιών του είναι 0,04 m.

γ)   Το σημείο Μ αποτελεί την πρώτη μετά την αρχή αξόνων κοιλία του στάσιμου κύματος.

δ)  Η μέγιστη ταχύτητα του Μ είναι 0,04 m/s

A.5. (Στις προτάσεις που ακολουθούν να σημειώσετε Σ στις σωστές και Λ στις λανθασμένες)

Συνέχεια:  Όλο το Διαγώνισμα - οι Απαντήσεις

Το "2ο Γενικό Διαγώνισμα στα κύματα" αναθεωρημένο και βελτιωμένο

Α.1. Ένα αρμονικό κύμα περιγράφεται από την εξίσωση:

                                             0,1ημ2π(2t -  x⁄20 ⁾    (S.I).

 H μεταβολή της φάσης της ταλάντωσης ενός σημείου του ελαστικού μέσου μεταξύ δύο χρονικών στιγμών που διαφέρουν κατά Δt = 1/6 sec, είναι ίση με:

                     α) 0,5π,          β) 2π/3,      γ) 1,5π,         δ)  2π 

Α.2.  Οι πηγές Π₁ και Π₂ είναι δύο σύγχρονες πηγές που δημιουργούν κύματα στην επιφάνεια ενός υγρού. Το σημείο Β βρίσκεται πάνω στην πρώτη, μετά τη μεσοκάθετο, ενισχυτική υπερβολή. Αυτό σημαίνει ότι όταν σ’ αυτό φτάνει ένα ¨όρος¨ που προέρχεται από την πηγή Π₂, ταυτόχρονα φτάνει και ένα ¨όρος¨ που προέρχεται από την πιο μακρινή πηγή Π₁, το οποίο:

α) ξεκίνησε ταυτόχρονα με το όρος της πηγής Π₂, 

β) ξεκίνησε μια περίοδο νωρίτερα,

γ) ξεκίνησε μια περίοδο αργότερα,

δ) ξεκίνησε μισή περίοδο νωρίτερα.

Α.3.  Οι νυχτερίδες μπορούν να εντοπίσουν μικρά αντικείμενα, π.χ. έντομα, με διαστάσεις τουλάχιστον ίσες με το μήκος κύματος των υπερήχων που εκπέμπουν. Αν μια νυχτερίδα εκπέμπει ένα τερέτισμα (κελαηδισμό) με συχνότητα 66 kHz και η ταχύτητα του ήχου στον αέρα είναι 330 m/sec, το μικρότερο μέγεθος εντόμου που μπορεί να εντοπίσει  είναι:

 α. 2 mm,      β. 0,5 mm,       γ. 0,2 mm,        δ. 5 mm

Α.4.  Σήμερα γνωρίζουμε ότι ο πυρήνας της γης αποτελείται από ένα εξωτερικό και ένα εσωτερικό τμήμα. Το εξωτερικό τμήμα του πυρήνα είναι σε ρευστή (υγρή) κατάσταση, ενώ το εσωτερικό είναι στερεό. Όταν γίνεται ένας σεισμός απελευθερώνεται ενέργεια, που είναι συσσωρευμένη στις λιθοσφαιρικές πλάκες του φλοιού της γής, και δημιουργούνται εγκάρσια και διαμήκη κύματα.  Οι σεισμογράφοι, που βρίσκονται σε αντιδιαμετρική θέση  ως προς την εστία ενός σεισμού καταγράφουν:

α) μόνο τα διαμήκη κύματα

β) μόνο τα εγκάρσια κύματα

γ) και τα διαμήκη και τα εγκάρσια

δ) ούτε τα διαμήκη, ούτε τα εγκάρσια.

Α.5. Χαρακτηρίστε καθεμιά από τις  παρακάτω προτάσεις ως σωστή ή λάθος:

α. Οποιαδήποτε κυματική διαταραχή, όσο περίπλοκη και να είναι, μπορεί να θεωρηθεί ότι προέρχεται από το άθροισμα ενός αριθμού αρμονικών κυμάτων.

β. Θα μπορούσαμε να ορίσουμε το μήκος κύματος ως την απόσταση μεταξύ δύο διαδοχικών σημείων του μέσου που οι απομακρύνσεις από τη θέση ισορροπίας τους και οι ταχύτητές τους είναι ίσες.

γ. Κύματα που διαδίδονται ταυτόχρονα στο ίδιο μέσον αλληλεπιδρούν μεταξύ τους.

δ. Η ενέργεια των κυμάτων από τη συμβολή των οποίων δημιουργείται στάσιμο κύμα εγκλωβίζεται ανάμεσα σε ζεύγη διαδοχικών δεσμών.

ε. Κατά τη διάδοση ενός κύματος τα μόρια του ελαστικού μέσου κινούνται γύρω από τη θέση ισορροπίας τους.

Συνέχεια:  Όλο το διαγώνισμα - Οι απαντήσεις

Περιοχές συμβολής επιφανειακών κυμάτων, η περίεργη ταλάντωση ενός φελλού και σημεία της επιφάνειας που την μιμούνται.

[Μια άσκηση που λύνεται  εύκολα αν στηριχτούμε στη λογική της σύνθεσης ταλαντώσεων και όχι στις γνωστές εξισώσεις συμβολής κυμάτων σε επιφάνεια υγρού.]

Στην επιφάνεια ενός υγρού υπάρχουν δύο σύγχρονες πηγές εγκαρσίων κυμάτων Π₁, Π₂ που αρχίζουν να ταλαντώνονται τη στιγμή t = 0 με εξισώσεις :

                          ψ₁ = ψ₂ = Aημ8πt,    (τα μεγέθη ψ και t στο S.I),

και παράγουν κύματα, τα οποία διαδίδονται με ταχύτητα υ=4 m/sec προς όλες τις διευθύνσεις της επιφάνειας του υγρού.

Υποθέτουμε ότι τα κύματα διαδίδονται χωρίς απώλεια ενέργειας. Καθώς, όμως, απλώνονται στην επιφάνεια, η ενέργεια που παρέχει η πηγή ανά περίοδο, μεταφέρεται από το κύμα και διαμοιράζεται συνεχώς σε σημεία όλο και μεγαλύτερων ομόκεντρων κύκλων και συνεπώς σε όλο και περισσότερα υλικά σημεία. Για αυτό, το πλάτος καθενός από τα κύματα μειώνεται με την απόσταση από τις πηγές.

Έστω ότι σε απόσταση 2,75 m  από κάθε πηγή το πλάτος ταλάντωσης, που κάθε σημείο υποχρεώνεται να κάνει, είναι ίσο με A₁ = 4 cm, ενώ σε απόσταση 3,25 m είναι ίσο με A₂ = 3,8 cm.

α. Να δικαιολογήσετε γιατί ένας φελλός, που βρίσκεται σε ένα σημείο Β στην επιφάνεια του υγρού σε απόσταση 3,25 m από τη μια πηγή και 2,75 m από την άλλη, θα ξεκινήσει τη στιγμή t₁ λίγο μετά την έναρξη ταλάντωσης των πηγών, θα κάνει μισή ταλάντωση με μηδενική αρχική φάση και πλάτος 4 cm κι ύστερα, από μια στιγμή t₂ και έπειτα, θα ξεκινήσει μια νέα ταλάντωση με αρχική φάση π και πλάτος 0,2 cm.

β. Να δείξετε, γραμμοσκιάζοντάς την, την περιοχή της επιφάνειας του υγρού όπου τις χρονικές στιγμές t₁ και t₂ έχουν συμβάλλει τα κύματα των δύο πηγών.

γ. Υπάρχουν και άλλα σημεία, που η κίνησή τους είναι πανομοιότυπη με αυτήν του Β. Πού βρίσκονται αυτά τη χρονική στιγμή t₂;

δ. Ποια σημεία της επιφάνειας του υγρού έχουν εκτελέσει περισσότερες ταλαντώσεις με πλάτος 0,2 m τη στιγμή t₂; 

 Απάντηση:

Αρμονικό κύμα: παρακολουθώντας την κίνηση μιας κορυφής

Kατά μήκος ενός γραμμικού ελαστικού μέσου, που η διεύθυνσή του ταυτίζεται με τον άξονα x΄x, έχει αναπτυχθεί ένα αρμονικό κύμα πλάτους Α. Θεωρούμε τη θέση ισορροπίας ενός σημείου Ο του ελαστικού μέσου ως αρχή των αξόνων x΄x και ψ΄ψ κι αρχίζουμε να μετράμε το χρόνο από κάποια στιγμή που το σημείο αυτό βρίσκεται στην πάνω ακραία θέση του. Έτσι, τη στιγμή t = 0, στην αρχή αξόνων βρίσκεται η κορυφή που δείχνεται με το κατακόρυφο βέλος.

α) Αν η ταχύτητα με την οποία μετακινείται η κορυφή αυτή είναι υ = 1 m/sec και αν η μέγιστη επιτάχυνση του σημείου Ο είναι 0,8π² m/sec², να βρείτε την εξίσωση του κύματος.

β) Σε ποια θέση βρίσκεται η παραπάνω κορυφή τη στιγμή που το σημείο Ο διέρχεται για έκτη φορά από τη θέση ισορροπίας του;

 (Τα παραπάνω στιγμιότυπα, για λόγους απλότητος, έχουν σχεδιαστεί σε ένα ορισμένο τμήμα του ελαστικού μέσου). 

Απάντηση:

Απώλεια ενέργειας ταλάντωσης σε μια ιδιαίτερη πλαστική κρούση. Ποσοτική και ποιοτική μελέτη

Δίνεται ο απλός αρμονικός ταλαντωτής του σχήματος: ένα σώμα Σ μάζας m, που βρίσκεται πάνω σε λείο οριζόντιο επίπεδο, και ένα ιδανικό οριζόντιο ελατήριο σταθεράς k = 100 Ν/m, που η μια του άκρη είναι δεμένη στο σώμα και η άλλη του άκρη είναι στερεωμένη ακλόνητα.

Το σώμα Σ κινείται μεταξύ των θέσεων Α και Β με πλάτος Α.

Από ύψος h αφήνουμε να πέσει ένα κομμάτι πλαστελίνης μάζας m, το οποίο προσκολλάται στο σώμα που ταλαντώνεται.

I. Σε ποια από τις παρακάτω θέσεις πρέπει να γίνει η κρούση ώστε η απώλεια της μηχανικής ενέργειας του συστήματος να είναι η μέγιστη δυνατή;

α. Σε μια ακραία θέση,    

β. Στη θέση ισορροπίας Ο,      

γ. Σε καμιά· η απώλεια μηχανικής ενέργειας είναι ίδια σε οποιαδήποτε θέση γίνει η κρούση.

ΙΙ. Να αιτιολογήσετε την απάντησή σας.

Η χρονική διάρκεια της κρούσης να θεωρηθεί αμελητέα. 

Απάντηση: