ΣΤΡΟΦΟΡΜΗ, ΔΙΑΤΗΡΗΣΗ, ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ - ΘΕΜΑ Β, ερώτηση 3η

3. Δύο σφαιρίδια αμελητέων διαστάσεων με σταθερή στροφορμή

 Δύο σφαιρίδια με ασήμαντες διαστάσεις έχουν ίσες μάζες m = 0,2 kgr και είναι στερεωμένα στα άκρα μιας αβαρούς οριζόντιας ράβδου μήκους ℓ = 2 m.

Στη μέση της ράβδου αυτής στερεώνουμε ένα ακλόνητο κατακόρυφο άξονα ο οποίος αποτελεί επίσης και τον άξονα περιστροφής ενός καρουλιού. Ο κύλινδρος του καρουλιού έχει ακτίνα R = 0,1 m και πάνω του είναι τυλιγμένο πολλές φορές ένα αβαρές μη ελαστικό νήμα που οδηγείται, οριζόντιο, στο αυλάκι μιας αβαρούς τροχαλίας η οποία μπορεί να στρέφεται γύρω από ακλόνητο άξονα. Στο τέλος του σχοινιού δένεται ένα σώμα Σ μάζας m₁ = 1 kgr.  Τριβές δεν υπάρχουν, ούτε το σχοινί ολισθαίνει στο καρούλι και στην τροχαλία. Τότε:

 Α.  Η ροπή που πρέπει να ασκήσουμε στο σύστημα σφαιρίδια – οριζόντια ράβδος – καρούλι ως προς τον κατακόρυφο άξονα περιστροφής, ώστε το σώμα Σ να ανεβαίνει με σταθερή ταχύτητα, έχει μέτρο:

Η συνέχεια της ερώτησης με αναλυτική απάντηση εδώ.

ΣΤΡΟΦΟΡΜΗ, ΔΙΑΤΗΡΗΣΗ, ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ - ΘΕΜΑ Β, ερώτηση 2η

2.  Ένα σφαιρίδιο αμελητέων διαστάσεων με σταθερή στροφορμή

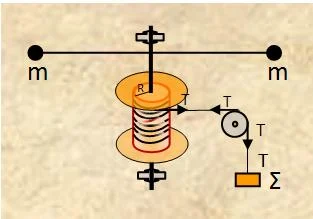
  Ένα σφαιρίδιο αμελητέων διαστάσεων εκτελεί, χωρίς τριβές, κυκλική κίνηση ακτίνας R, όπως φαίνεται στο σχήμα. Τραβάμε το σχοινί και μειώνουμε την ακτίνα περιστροφής του σφαιριδίου στο μισό. Τότε η γωνιακή ταχύτητα περιστροφής του σφαιριδίου γύρω

από το κέντρο της κυκλικής τροχιάς:

α) παραμένει ίδια.

β) διπλασιάζεται.

γ) υποδιπλασιάζεται

δ) τετραπλασιάζεται.

Να δικαιολογήσετε την απάντησή σας.

Η ερώτηση μαζί με την απάντηση σε pdf εδώ.

ΣΤΡΟΦΟΡΜΗ, ΔΙΑΤΗΡΗΣΗ, ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ - ΘΕΜΑ Β ερώτηση 1η

1. Μια περίπτωση διατήρησης στροφορμής με συνέπειες … σε όσους δε ζaλίζονται

  Κυκλική οριζόντια πλατφόρμα μπορεί να περιστρέφεται χωρίς τριβές γύρω από κατακόρυφο άξονα που διέρχεται από το κέντρο της. Δύο παιδιά στέκονται ακίνητα στις άκρες μιας διαμέτρου της πλατφόρμας. Το σύστημα πλατφόρμα – παιδιά στρέφεται αρχικά με σταθερή γωνιακή ταχύτητα ω. Κάποια στιγμή τα δύο παιδιά αρχίζουν να πλησιάζουν προς τον άξονα περιστροφής.

Τότε η στροφορμή κάθε παιδιού ως προς τον άξονα περιστροφής:

α)  αυξάνεται,                   

β)  μειώνεται, 

γ)  παραμένει σταθερή,    

δ)  μεταβάλλεται μόνο ως προς τον προσανατολισμό.

Η ερώτηση και η αναλυτική απάντηση σε pdf εδώ.

ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΤΗΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ – ΘΕΜΑ Β

 Ομογενής κύλινδρος μάζας m και ακτίνας R μπορεί να περιστρέφεται γύρω από σταθερό ά­ξονα, που ταυτίζεται με τον άξονα συμμετρίας του. Η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα αυτόν είναι Ι = mR²/2.  Γύρω από τον κύλινδρο είναι τυλιγμένο νήμα στο ελεύθερο άκρο του οποίου είναι δεμένο ένα σώμα μά­ζας m ίδιας με του κυλίνδρου. Αφήνουμε το σώμα να κινηθεί κατακόρυφα προς τα κάτω. To νήμα ασκεί στον κύλινδρο εφαπτομενική δύναμη Τ και ξετυλίγεται, περιστρέφοντάς τον. Δίνεται και η επιτάχυνση βαρύτητας g.

 

Σε κάθε αριθμό της στήλης Α του παρακάτω πίνακα να αντιστοιχίσετε ένα γράμμα της στήλης Β. ...

Δείτε τη συνέχεια μαζι με τις υπόλοιπες ερωτήσεις εδώ και αναλυτικές απαντήσεις εδώ.

ΚΥΛΙΣΗ ΧΩΡΙΣ KAI ME ΟΛΙΣΘΗΣΗ ΣΕ ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ ΩΣ ΑΠΟΤΕΛΕΣΜΑ ΤΗΣ ΤΑΥΤΟΧΡΟΝΗΣ ΔΡΑΣΗΣ ΒΑΡΟΥΣ ΚΑΙ ΤΡΙΒΗΣ

Ένα δαχτυλίδι, ένας κύλινδρος και ένα συμπαγές σφαιρίδιο, φτιαγμένα από ομογενή υλικά, αφήνο­νται να κυλήσουν ταυτόχρονα από το ίδιο ύψος  ενός κεκλιμένου επιπέδου. Αν η κύλιση γίνεται χωρίς ολίσθηση, να δείξετε ότι όποια κι αν είναι η σχέση μαζών των σωμάτων και όποια κι αν είναι η σχέση των ακτίνων τους, το σφαιρίδιο θα φτάσει γρηγορότερα στη βάση το πλάγιου επιπέδου.

Θεωρείστε ότι η ροπή αδράνειας και των τριών σωμάτων ως προς τον ελεύθερο άξονα περιστροφής τους, που διέρχεται από το κέντρο μάζας τους, αποδίδεται από τη σχέση:

 I_c = λmR²

όπου m και R είναι η μάζα και η ακτίνα των παραπάνω σωμάτων (με διαφορετικές τιμές για το καθένα), και λ ένας αριθμητικός συντελεστής που η τιμή του είναι 1 για το δακτυλίδι, 0,5 για τον κύλινδρο και 0,4 για το σφαιρίδιο, αντίστοιχα.

Απάντηση:

ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ – ΘΕΜΑ Α

1. Ανομοιογενής ράβδος μήκους L ηρεμεί σε λείο οριζόντιο επίπεδο. Τη χρονική στιγμή  t = 0 αρχίζει να ενεργεί πάνω της ζεύγος οριζοντίων δυνάμενων F₁= F₂ = F, που διατηρούνται διαρκώς κάθετες στη ράβδο, όπως στο σχήμα. 

Α. Οι ρυθμοί μεταβολής της ταχύτητας του κέντρου μάζας (C) και της γωνιακής ταχύτητας της ράβδου είναι, αντίστοιχα:

        i.       μηδέν και διάφορος του μηδενός

        ii.     διάφορος του μηδενός και μηδέν

        iii.    μηδέν και μηδέν.

Β. Αν Ι_c είναι η ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος σ’ αυτήν, τότε η γωνιακή ταχύτητα και το μέτρο της γραμμικής ταχύτητας του γεωμετρικού μέσου (Κ) της ράβδου τη χρονική στιγμή t είναι, αντίστοιχα:

Η συνέχεια εδώ και οι αναλυτικές απαντήσεις εδώ.

ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ ΚΑΙ ΙΣΟΡΡΟΠΙΑ - ΘΕΜΑ Β

1. Μια ομογενής και σταθερής διατομής ράβδος, μήκους ℓ = 3 m, ισορροπεί οριζόντια. Το ένα άκρο της είναι αρθρωμένο σε κατακόρυφο τοίχο, ενώ το άλλο είναι στερεωμένο στο κατώτερο άκρο ενός κατακόρυφου ελατηρίου με σταθερά k = 100 Ν/m, στο οποίο έχει προκαλέσει επιμήκυνση Δℓ = 40 cm. Να βρείτε τη ροπή αδράνειας της ράβδου ως προς το άκρο της Ο.

Δίνεται η σχέση της ροπής αδράνειας λεπτής ομογενούς ράβδου ως προς το κέντρο μάζας της: I_c.m = mℓ ²/12 και η επιτάχυνση βαρύτητας g = 10 m/sec².

                                                                                                                Απ. 24 kgr.m²

Εδώ θα βρείτε τις  υπόλοιπες ερωτήσεις κι εδώ αναλυτικές απαντήσεις.