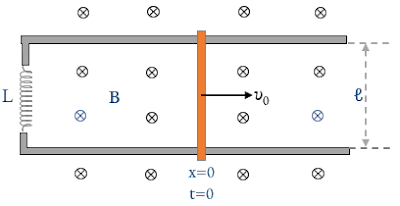
Δύο παράλληλες αγώγιμες ακλόνητες
ράγες μεγάλου μήκους και αμελητέας αντίστασης χωρίζονται με απόσταση ℓ. Δύο πανομοιότυπες αγώγιμες ράβδοι
τοποθετούνται στις ράγες κάθετα σε αυτές. Το όλο σύστημα βρίσκεται σε οριζόντιο
επίπεδο. Κάθε ράβδος έχει μάζα M και ωμική αντίσταση R.
Υπάρχει παντού ένα ομογενές μαγνητικό πεδίο που κατευθύνεται κάθετα προς στο
επίπεδο της όλης διάταξης. Στη μία από τις δύο ράβδους δίνεται αρχική ταχύτητα υ0
παράλληλη προς τις ράγες και με κατεύθυνση τέτοια ώστε να απομακρυνθεί αρχικά
από την άλλη.
Απαντήστε στις ακόλουθες
ερωτήσεις για το σύστημα των δύο ράβδων (αγνοείστε την τριβή και την αυτεπαγωγή):
α. Δείξτε ότι
κάποτε οι δύο αγωγοί θα αποκτήσουν κοινή σταθερή ταχύτητα.
β. Θα μειωθεί
η ορμή του συστήματος με το χρόνο;
γ. Ποια είναι
η κινητική ενέργεια του συστήματος σε σταθερή κατάσταση;
Η λύση με κλικ εδώ