| ΚΑΝΟΝΙΚΕΣ | ΕΠΑΝΑΛΗΠΤΙΚΕΣ | ΚΑΝΟΝΙΚΕΣ | ΕΠΑΝΑΛΗΠΤΙΚΕΣ | ΚΑΝΟΝΙΚΕΣ |
| 2000 | 2000 | 2000 | ||
| 2001 | 2001 | 2001 | ||
| 2002 | 2002 | 2002 | ||
| 2003 | 2003 | 2003 | 2003 | |
| 2004 | 2004 | 2004 | 2004 | |
| 2005 | 2005 | 2005 | 2005 | |
| 2006 | 2006 | 2006 | ||
| 2007 | 2007 | 2007 | ||
| 2008 | 2008 | 2008 | ||
| 2009 | 2009 | |||
| 2010 | 2010 | |||
| 2011 | 2011 | |||
| 2012 | 2012 | 2012 | ||
| 2013 | 2013 | |||
| 2014 | 2014 | |||
Στο χώρο αυτό, οι μαθητές της Γ Λυκείου αλλά και οι συνάδελφοι εκπαιδευτικοί θα βρουν μια σειρά από ερωτήσεις, πρωτότυπες ασκήσεις και προβλήματα στο πνεύμα των πανελλαδικών εξετάσεων. Το υλικό δημιουργήθηκε μέσα από χρόνια δουλειάς με μαθητές και συναδέλφους. μπορεί όμως ακόμη να έχει κάποιες ατέλειες. Kάθε καλοπροαίρετη παρατήρηση ή διόρθωση δεν είναι τυπικό σχόλιο· είναι μια μικρή, ουσιαστική συμβολή σε μια δουλειά που εξακολουθεί να εξελίσσεται μαζί σας.
Η φύση αγαπά την αλήθεια, και η αλήθεια της φύσης διεκδικεί το δικαίωμα να εκτίθεται μόνο σε όσους την ποθούν. (Φ. Ντοστογιέφσκι)
🏠 Αρχική
Home
💥 Κρούσεις
Collisions
📈 Ταλαντώσεις
Oscillations
🌊 Κύματα
Waves
⚙️ Μηχανική Στερεού
Rigid Body
🧲 Ηλεκτρομαγνητισμός
Electromagnetism
🌀 Κβαντομηχανική
Quantum Physics
🔧 Ρευστά σε κίνηση
Fluids
🌐 Exams Preparation Portal
Entrance Portal
📚 Τράπεζα Θεμάτων
Topic Bank
🧭 Πλοήγηση
Advanced Navigation
📚 Βιβλιοθήκες
Libraries
- ΤΡΑΠ.ΘΕΜ.Α ΛΥΚ
- ΤΡΑΠ.ΘΕΜ.Β ΛΥΚ
- Global Physics Entrance Portal
- Αρχική σελίδα
- Νέα τράπεζα θεμάτων φυσικής Β Λυκείου ανά κεφάλαιο
- Βιντεοδιαλέξεις, Μαθήματα & Διαγωνισμοί
- Richard Feynman
- Quantum Mechanics
- Tree-Hour Test 2
- Three-hour test 1
- Three-Hours Test 3
- Greek National Physics Exams — Problems & Solutions — 2002–2025
- Greek National Physics Exams — Problems & Solutions — 2002–2025
- Three-hour Tests
- High School 1st Year Exam Questions Bank
- Physics B' Lyceum: Strategic Question Bank for Greek University Entrance Exams
- Physics C' Lyceum: Strategic Question Bank for Greek University Entrance Exams
- Physics National Exams Simulations
- Federation of Greek Teachers
- Keystone We are in
- General Education Physics exams— Problems & Solutions (2000 - 2016)
- OEFE and Keystone simulation exams
- My Digital Lbrary
- Physics Exam Preparation Portal
- Second Library
Δευτέρα 2 Μαΐου 2011
ΤΑ ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 2000 - 2014
Σάββατο 30 Απριλίου 2011
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ – 33 ΕΠΑΝΑΛΗΠΤΙΚΑ ΤΕΣΤ
Τριάντα τρία τεστ από το σχολικό βιβλίο και όχι μόνο.
Παρασκευή 29 Απριλίου 2011
ΚΡΟΥΣΕΙΣ – ΦΑΙΝΟΜΕΝΟ DOPPLER. ΤΕΤΡΑΔΙΟ ΜΕ ΤΙΣ ΑΣΚΗΣΕΙΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ
Μπορείτε να κατεβάσετε το τετράδιο με αριστερό κλικ εδώ!
Τρίτη 26 Απριλίου 2011
ΔΑΚΤΥΛΙΟΣ - ΤΡΕΙΣ ΡΑΒΔΟΙ - ΣΦΑΡΙΔΙΟ
Δακτύλιος - τρείς ράβδοι - σφαιρίδιο
Ο τροχός του σχήματος αποτελείται από ένα κατακόρυφο δακτύλιο αμελητέου πάχους, από ένα σφαιρίδιο το οποίο είναι προσκολλημένο σε ένα σημείο Σ του δακτυλίου και από τρεις ράβδους με μήκος ℓ ίσο με την ακτίνα του δακτυλίου. Οι ράβδοι είναι συγκολλημένες κι αυτές στο δακτύλιο ώστε να αποτελούν τρείς ακτίνες του, που ανά δύο να σχηματίζουν γωνία ίση με 120ο . Ο τροχός μπορεί να περιστρέφεται γύρω από ακλόνητο οριζόντιο άξονα που είναι κάθετος πάνω του και διέρχεται από το κέντρο του Κ.
Ο δακτύλιος, καθεμιά ράβδος και το σφαιρίδιο έχουν την ίδια μάζα m. Αρχικά, συγκρατούμε τον τροχό με την ακτίνα ΚΣ σε οριζόντια θέση. Ύστερα τον αφήνουμε ελεύθερο να περιστραφεί γύρω από τον οριζόντιο άξονα.
α) Πόση είναι η αρχική γωνιακή επιτάχυνση του τροχού;
β) Πόσος είναι ο αρχικός ρυθμός μεταβολής της στροφορμής σφαιριδίου;
γ) Πόση είναι η γωνιακή ταχύτητα του τροχού τη στιγμή που η ακτίνα ΚΣ γίνεται κατακόρυφη;
Οι απαντήσεις σας να δοθούν σε συνάρτηση με την επιτάχυνση βαρύτητας g, το μήκος ℓ των ράβδων και τη μάζα m.
Δίνεται η ροπή αδράνειας κάθε ράβδου ως προς το κέντρο μάζας της:
Ιc.m = m ℓ2/ 12.
Δευτέρα 25 Απριλίου 2011
ΣΤΡΟΦΟΡΜΗ, ΔΙΑΤΗΡΗΣΗ, ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ - ΘΕΜΑ Β ερώτηση 4η
4. Ένας ρυθμός μεταβολής στροφορμής και κάποιοι προβληματισμοί.
Στο άκρο Α της ράβδου ΟΑ (μάζας m και μήκους ℓ, ομογενής και ισοπαχής, με Ic.m = mℓ 2/12) έχουμε στερεώσει ένα σφαιρίδιο αμελητέας ακτίνας με μάζα m ίδια με της ράβδου.
Αφήνουμε τη ράβδο από τη θέση που φαίνεται στο σχήμα (οριζόντια) να στραφεί ελεύθερα, χωρίς τριβές, σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα που διέρχεται από το άκρο της Ο.
O αρχικός ρυθμός μεταβολής της στροφορμής του σφαιριδίου ως προς τον άξονα αυτόν έχει μέτρο:
α) mgℓ, γ) 9mgℓ /8,
β) mgℓ /2 δ) 3mgℓ /2
Να δικαιολογήσετε την απάντησή σας.
Η ερώτηση με την αναλυτική απάντηση σε pdf εδώ και κάποιοι προβληματισμοί εδώ.Σάββατο 23 Απριλίου 2011
ΣΤΡΟΦΟΡΜΗ, ΔΙΑΤΗΡΗΣΗ, ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ - ΘΕΜΑ Β, ερώτηση 3η
3. Δύο σφαιρίδια αμελητέων διαστάσεων με σταθερή στροφορμή
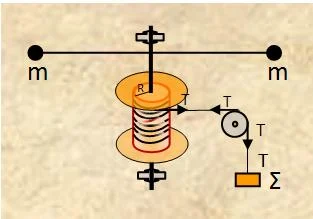
Δύο σφαιρίδια με ασήμαντες διαστάσεις έχουν ίσες μάζες m = 0,2 kgr και είναι στερεωμένα στα άκρα μιας αβαρούς οριζόντιας ράβδου μήκους ℓ = 2 m.
Στη μέση της ράβδου αυτής στερεώνουμε ένα ακλόνητο κατακόρυφο άξονα ο οποίος αποτελεί επίσης και τον άξονα περιστροφής ενός καρουλιού. Ο κύλινδρος του καρουλιού έχει ακτίνα R = 0,1 m και πάνω του είναι τυλιγμένο πολλές φορές ένα αβαρές μη ελαστικό νήμα που οδηγείται, οριζόντιο, στο αυλάκι μιας αβαρούς τροχαλίας η οποία μπορεί να στρέφεται γύρω από ακλόνητο άξονα. Στο τέλος του σχοινιού δένεται ένα σώμα Σ μάζας m1 = 1 kgr. Τριβές δεν υπάρχουν, ούτε το σχοινί ολισθαίνει στο καρούλι και στην τροχαλία. Τότε:
Α. Η ροπή που πρέπει να ασκήσουμε στο σύστημα σφαιρίδια – οριζόντια ράβδος – καρούλι ως προς τον κατακόρυφο άξονα περιστροφής, ώστε το σώμα Σ να ανεβαίνει με σταθερή ταχύτητα, έχει μέτρο:
Η συνέχεια της ερώτησης με αναλυτική απάντηση εδώ.
ΣΤΡΟΦΟΡΜΗ, ΔΙΑΤΗΡΗΣΗ, ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ - ΘΕΜΑ Β, ερώτηση 2η
2. Ένα σφαιρίδιο αμελητέων διαστάσεων με σταθερή στροφορμή
 Ένα σφαιρίδιο αμελητέων διαστάσεων εκτελεί, χωρίς τριβές, κυκλική κίνηση ακτίνας R, όπως φαίνεται στο σχήμα. Τραβάμε το σχοινί και μειώνουμε την ακτίνα περιστροφής του σφαιριδίου στο μισό. Τότε η γωνιακή ταχύτητα περιστροφής του σφαιριδίου γύρω
Ένα σφαιρίδιο αμελητέων διαστάσεων εκτελεί, χωρίς τριβές, κυκλική κίνηση ακτίνας R, όπως φαίνεται στο σχήμα. Τραβάμε το σχοινί και μειώνουμε την ακτίνα περιστροφής του σφαιριδίου στο μισό. Τότε η γωνιακή ταχύτητα περιστροφής του σφαιριδίου γύρω από το κέντρο της κυκλικής τροχιάς:
α) παραμένει ίδια.
β) διπλασιάζεται.
γ) υποδιπλασιάζεται
δ) τετραπλασιάζεται.
Να δικαιολογήσετε την απάντησή σας.
Εγγραφή σε:
Σχόλια (Atom)