Η προφανής και η «αφανής» στατική τριβή στη μη ολίσθηση

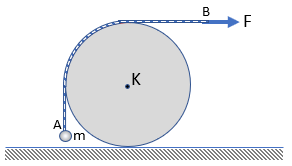
Στο σχήμα φαίνεται η εγκάρσια κατακόρυφη τομή ενός οριζόντιου ομογενούς κυλίνδρου, που το κέντρο της ταυτίζεται με το κέντρο μάζας του κυλίνδρου. Ένα μικρό σώμα μάζας m κρατιέται σε ισορροπία δεμένο στην άκρη Α ενός σχοινιού αμελητέας μάζας, του οποίου ένα τμήμα εφάπτεται στον κύλινδρο, όπως φαίνεται στο σχήμα. Η άλλη άκρη B του σχοινιού τραβιέται από μια οριζόντια δύναμη F. Αν το σχοινί δεν ολισθαίνει στην επιφάνεια του κυλίνδρου και ο κύλινδρος ηρεμεί στην οριζόντια επιφάνεια, το μέτρο της F είναι ίσο με:

                                       α)  mg/2            β) mg,             γ)  3mg/2

Σύντομη απάντηση: 
Αναλυτική απάντηση σε pdf: 
Αναλυτική απάντηση σε word:

Περιστροφή δίσκου γύρω από οριζόντια χορδή του

Ένας ομογενής κυκλικός δίσκος έχει ακτίνα R και μάζα m. Ένα σωματίδιο, επίσης μάζας m, είναι στερεωμένο στο σημείο Σ στην άκρη του δίσκου όπως φαίνεται στο σχήμα. Ο δίσκος μπορεί να περιστρέφεται χωρίς τριβές γύρω από τον σταθερό οριζόντιο άξονα ΡΡ΄, πάνω στον οποίο βρίσκεται η χορδή ΑΒ που απέχει R / 4 από το κέντρο Κ του δίσκου και είναι κάθετη στην προέκταση της ακτίνας ΣΚ. Αρχικά, ο δίσκος κρατείται κατακόρυφα με το σωματίδιο στο σημείο Σ στην υψηλότερη θέση του. Στη συνέχεια αφήνεται να πέσει, έτσι ώστε να αρχίσει να περιστρέφεται γύρω από τοnν άξονα PΡ΄. 

Βρείτε τη γραμμική ταχύτητα του σωματιδίου καθώς φθάνει στη χαμηλότερη θέση του.

Δίνεται ότι η ροπή αδράνειας ομογενούς κυκλικού δίσκου ως προς άξονα που βρίσκεται στο επίπεδό του και διέρχεται από το κέντρο του είναι I = mR²/4. 

Απάντηση σε pdf 
Απάντηση σε word:

Κατακόρυφη περιστροφή ράβδου στο εσωτερικό κοίλου κυλίνδρου

[Εδώ, μια ράβδος στρέφεται γύρω από άξονα που δεν διέρχεται από το φορέα της]

Θεωρείστε ένα κοίλο κύλινδρο σταθερό σε οριζόντιο επίπεδο, με λεία εσωτερική επιφάνεια ακτίνας     R = 5 m και μια ομογενή ράβδο μάζας M και μήκους L = 8 m, που συγκρατείται αρχικά σε κατακόρυφη θέση όπως φαίνεται στο σχήμα. Κάποια στιγμή η ράβδος αφήνεται από τη θέση αυτή   και αρχίζει να γλιστράει μέσα στον κύλινδρο με τα άκρα της διαρκώς σε επαφή με τα εσωτερικά τοιχώματά του.

Θεωρείστε ότι κατά την πτώση της η ράβδος βρίσκεται διαρκώς στο ίδιο κατακόρυφο επίπεδο και    ότι η κίνησή της είναι καθαρά στροφική γύρω από τον άξονα του κυλίνδρου που διέρχεται από το O.

Υπολογίσετε τη γωνιακή ταχύτητα της ράβδου τη στιγμή που γίνεται οριζόντια.

Δίνεται για  τη ράβδο η ροπή αδράνειας Ι_c.m = (1/12)ML²_.

Θεωρείστε, για ευκολία, ότι g = 86/9 m/s².

Απ.  2r/s
Λύση σε pdf:  

Λύση σε word:

Μεταβάλλει η σανίδα την απόσταση ανάμεσα στους δυο κυλίνδρους;

Στο σχήμα η σανίδα που στηρίζεται στους δύο κυλίνδρους είναι οριζόντια. Τραβάμε τη σανίδα προς τα δεξιά έτσι ώστε το κέντρο του μικρότερου κυλίνδρου να κινείται με σταθερή ταχύτητα v. Η τριβή είναι αρκετά μεγάλη ώστε να αποτρέπει την ολίσθηση σε όλες τις επιφάνειες. Να βρείτε:

α) Αν οι δύο κύλινδροι θα πλησιάσουν ο ένας τον άλλον, θα απομακρυνθούν ή θα διατηρήσουν σταθερή τη μεταξύ τους απόσταση.

β) Το λόγο των επιταχύνσεων των σημείων επαφής των δύο κυλίνδρων με τη σανίδα.

γ) Αν η σανίδα μετατοπιστεί κατά 2πR πόσες περιστροφές θα έχει κάνει κάθε κύλινδρος;

Απάντηση σε pdf:  

Απάντηση σε word:

Είναι δυνατό δύο ομογενείς σφαίρες σε επαφή να ισορροπούν μόνες τους πάνω σε πλάγιο επίπεδο;

[Μια ομογενής σφαίρα μόνη της, προφανώς, δεν μπορεί να ισορροπήσει σε πλάγιο επίπεδο. Δύο όμως;]

Δύο ομογενείς σφαίρες Α και Β έχουν τοποθετηθεί πάνω σε ένα πλάγιο επίπεδο έτσι ώστε να εφάπτονται μεταξύ τους. Παρατηρούμε ότι παραμένουν σε ισορροπία. Οι ακτίνες των δύο σφαιρών είναι ίσες. Ποια σφαίρα έχει μεγαλύτερη μάζα; 

Απάντηση σε pdf:  
Απάντηση σε word:

Ισορροπία τροχού με ενσωματωμένο ταλαντωτή

[Ο σημαντικός ρόλος της δύναμης  του ελατηρίου στο σημείο στήριξής του.]

Ένας τροχός μπορεί να περιστρέφεται ελεύθερα σε κατακόρυφο επίπεδο, γύρω από ακλόνητο κεντρικό οριζόντιο άξονα, χωρίς τριβή.

Υπάρχει μια οριζόντια ελαφριά ράβδος στερεωμένη στον τροχό κάτω από τον άξονα σε απόσταση d από αυτόν και ένα μικρός δακτύλιος μάζας m που μπορεί να ολισθαίνει κατά μήκος της ράβδου χωρίς τριβή. Ο δακτύλιος συνδέεται με ένα ελαφρύ ελατήριο. Το άλλο άκρο του ελατηρίου στερεώνεται στο χείλος του τροχού, όπως φαίνεται στο σχήμα. Αρχικά ο δακτύλιος  ισορροπεί στο κέντρο της ράβδου και το ελατήριο έχει το φυσικό του μήκος. Κρατάμε τον τροχό ώστε η ράβδος να παραμείνει οριζόντια, μετακινούμε προς τα δεξιά τον δακτύλιο και το ελατήριο συμπιέζεται.

Κάποια στιγμή ελευθερώνουμε ταυτόχρονα τον τροχό και τον δακτύλιο.  

α) Είναι δυνατόν ο τροχός να μην περιστρέφεται καθώς ο δακτύλιος εκτελεί α.α.τ. στη ράβδο;

β) Βρείτε την τιμή της σταθεράς ελατηρίου k ώστε η κατάσταση που περιγράφεται στο (α) να είναι δυνατή. 

Απάντηση σε pdf: 

Τροχαλία και κουβάς

[Εφαρμογή της Α.Δ.Ε όταν ο κουβάς αφήνεται ελεύθερος να κατέβει.]

Χρησιμοποιήστε την αρχή διατήρησης της ενέργειας  για να υπολογίσετε τη γωνιακή ταχύτητα της τροχαλίας που φαίνεται στο σχήμα, τη στιγμή που ο κάδος μάζας m = 3 kg έχει κατέλθει κατά h = 3 m, ξεκινώντας από την ηρεμία. Θεωρείστε αμελητέα τη μάζα του σχοινιού που είναι προσαρτημένο στον κάδο και τυλιγμένο πολλές φορές γύρω από την τροχαλία και ότι δεν γλιστρά καθώς ξετυλίγεται.

Η τροχαλία περιστρέφεται χωρίς τριβές.

Δίνεται η μάζα Μ = 4 kg, η ακτίνα R = 0,6 m και η ροπή αδράνειας I = MR²/2 της  τροχαλίας καθώς και ότι η επιτάχυνση βαρύτητας ισούται με g = 10 m/s². 

Απάντηση: