Όπου οι τριβές είναι στο όριό τους

Δύο παρόμοιοι ξύλινοι κύβοι, βάρους w = 15 N, υποστηρίζονται από μια αβαρή ράβδο με κλίση 45^ο ως προς το οριζόντιο επίπεδο, όπως φαίνεται στο σχήμα. Αν και οι δύο κύβοι βρίσκονται σε κατάσταση οριακής ισορροπίας* και ο συντελεστής οριακής στατικής τριβής (μ_w) μεταξύ του κύβου Β και το τοίχου είναι 0,5, τότε:

“Υγρή” ταλάντωση

Ο ανοικτός και στις δύο βάσεις  του κατακόρυφος κυλινδρικός σωλήνας του σχήματος, σταθερής διατομής Α, συγκρατείται ημιβυθισμένος σε μια δεξαμενή μεγάλης επιφάνειας γεμάτη με νερό. Αρχικά το σύστημα “σώμα Σ – έμβολο” ισορροπεί όπως στο σχήμα (α).

Αφήνουμε ελεύθερο το σώμα Σ, το έμβολο ανέρχεται και νερό εισχωρεί στον σωλήνα.

Αν δεν υπάρχουν απώλειες λόγω τριβών και αν η μάζα του εμβόλου είναι αμελητέα, να δείξετε ότι:

α. Υπάρχει θέση, όπου η ταχύτητα του σώματος Σ γίνεται μέγιστη και να βρείτε την απόστασή της από την αρχική του θέση.

Αναρρόφηση νερού σε μέγιστο ύψος με τη βοήθεια εμβόλου

Αναφερόμαστε στην  προηγούμενη άσκηση, με τη διαφορά ότι τώρα το κάτω ανοικτό άκρο του κατακόρυφου σωλήνα συγκρατείται ημιβυθισμένο σε μια δεξαμενή μεγάλης επιφάνειας, γεμάτη με νερό. Αρχικά το σύστημα “σώμα Σ – έμβολο” ισορροπεί όπως στο σχήμα (α).

Αφήνουμε ελεύθερο το σώμα Σ, το έμβολο ανέρχεται και νερό εισχωρεί στον σωλήνα.

Αν δεν υπάρχουν απώλειες λόγω τριβών και αν η μάζα του εμβόλου είναι αμελητέα σε σχέση με τη μάζα m του σώματος Σ, τότε το μέγιστο ύψος στο οποίο θα φτάσει το νερό στο σωλήνα, μετρούμενο από την επιφάνεια

Άντληση νερού και ισορροπία

Το έμβολο του σχήματος εφαρμόζει αεροστεγώς στα εσωτερικά τοιχώματα ενός κατακόρυφου κυλινδρικού σωλήνα, που είναι ανοικτός και στα δύο του άκρα και μπορεί να κινείται μέσα σε αυτόν χωρίς τριβές. Στην αρχή ισορροπεί στη θέση που φαίνεται στο σχήμα (α), με τη βοήθεια ενός σχοινιού στην άλλη άκρη του οποίου έχουμε κρεμάσει ένα σώμα Σ μάζας m. Αρχικά συγκρατούμε το σώμα για να μην κινηθεί προς τα κάτω. Ο σωλήνας είναι ημιβυθισμένος μέσα σε ένα δοχείο που περιέχει νερό όγκου 2L. Αφήνουμε σιγά – σιγά το σώμα Σ να κατέβει, με αποτέλεσμα το έμβολο να ανέβει και να εισέλθει νερό μέσα στο σωλήνα.

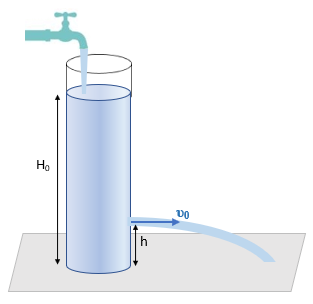
Σταθεροποίηση στάθμης και βεληνεκούς με δύο τρόπους. Ένα ακόμη θέμα Β στα ρευστά

Το κυλινδρικό δοχείο του σχήματος περιέχει νερό, του οποίου η ελεύθερη επιφάνεια φτάνει σε ύψος  Η₀ από τη βάση του.  Ανοίγουμε μια τρύπα εμβαδού α m² σε ύψος h < H₀/2 και το νερό αρχίζει να εκτινάσσεται από αυτήν με αρχική οριζόντια ταχύτητα πέφτοντας τελικά στο έδαφος. Ταυτόχρονα, ανοίγουμε μια βρύση και αρχίζουμε να παρέχουμε νερό στο δοχείο με σταθερή παροχή Π_β = α√2gh  m³/s.
 Ι. Η  στάθμη του νερού στο δοχείο:

α. Παραμένει στο ύψος Η₀.

β. Αρχίζει να πέφτει και κάποια στιγμή σταθεροποιείται σε ύψος 2h.

γ. Αρχίζει να πέφτει και κάποια στιγμή σταθεροποιείται στο ύψος h.

ΙΙ. Το βεληνεκές της φλέβας:

Τρία πρωτότυπα θέματα Β στα ρευστά 1. Η κούπα του Πυθαγόρα

Στο σχήμα (α) έχουμε σχεδιάσει την «κούπα του Πυθαγόρα», όπου μέσω ενός ανοίγματος, το υγρό που προσθέτουμε, εκτός από τον εμφανή χώρο στο εσωτερικό του κυπέλλου, εισχωρεί και στο κατακόρυφο “κρυφό” κανάλι ΔΕ (σχήμα β), το οποίο επικοινωνεί με δεύτερο ανοικτό κατακόρυφο κανάλι ΕΖ σταθερής διατομής. Αυτό διατρέχει τον κορμό του κύπελου και καταλήγει σε ένα άνοιγμα (στο σημείο Ζ) της βάσης του. Έτσι, αν η στάθμη του υγρού είναι χαμηλότερα από το σημείο Ε, δηλαδή ως το ύψος h (σχήματα β, γ), αυτό παραμένει μέσα στο κύπελλο, αν όμως ξεπεράσει το σημείο Ε τότε το υγρό οδηγείται στο κανάλι ΕΖ και από εκεί βγαίνει έξω από το κύπελλο, από το άνοιγμα της βάσης του στο σημείο Ζ.

 
Στο σχήμα (δ), ένα ιδανικό υγρό πυκνότητας ρ ισορροπεί μέσα σε ένα τέτοιο κύπελλο με τη στάθμη του σε ύψος Η > h, δεν χύνεται όμως γιατί  έχουμε σφηνώσει ένα κομμάτι φελλού στο άνοιγμα της βάσης του κύπελου.  Στη συνέχεια αφαιρούμε το φελλό και το υγρό αρχίζει να ρέει στο κανάλι ΔΕΖ και να εξέρχεται από το Ζ.

Τι από τα παρακάτω θα συμβεί:

2. Δύο πίδακες που εκτινάσσονται οριζόντια από δύο διαφορετικά βάθη h1 και h2 συναντιούνται σε βάθος h1+h2

Δύο πίδακες που εκτινάσσονται οριζόντια από δύο διαφορετικά βάθη h₁ και h₂ συναντιούνται. Στην άσκηση αυτή θα δούμε τι αντιπροσωπεύουν οι παραστάσεις: 

	_______
h1 + h2  και  2 √	h1h2

Άσκηση:

Το ανοικτό δοχείο του σχήματος περιέχει νερό. Σε δύο σημεία E και Z της ίδιας κατακορύφου του τοιχώματος του δοχείου και σε βάθη h₁ και h₂, αντίστοιχα, ανοίγουμε δύο οπές πολύ μικρής διατομής από τις οποίες εκτοξεύονται δύο πίδακες νερού.

Ι. Η απόσταση y_Σ, του σημείου συνάντησης Σ των δύο πιδάκων από την επιφάνεια του νερού, είναι ίση με:

	_______
α. 2(h1 - h2),       β.  h1 + h2        γ. 2√	h1h2