Στο χώρο αυτό, οι μαθητές της Γ Λυκείου αλλά και οι συνάδελφοι εκπαιδευτικοί θα βρουν μια σειρά από ερωτήσεις, πρωτότυπες ασκήσεις και προβλήματα στο πνεύμα των πανελλαδικών εξετάσεων. Το υλικό έχει ελεγχτεί και έχει πάρει την τελική του μορφή με τη συμβολή φίλων συνεργατών και ενός μεγάλου αριθμού μαθητών μου, μπορεί όμως ακόμη να έχει κάποιες ατέλειες. Οποιοδήποτε καλοπροαίρετο σχόλιο ή οποιαδήποτε διόρθωση είναι επιθυμητή.
Η φύση αγαπά την αλήθεια, και η αλήθεια της φύσης διεκδικεί το δικαίωμα να εκτίθεται μόνο σε όσους την ποθούν. Φ. Ντοστογιέφσκι
Σάββατο 15 Σεπτεμβρίου 2012
ΜΕΓΙΣΤΗ ΠΡΟΣΦΕΡΟΜΕΝΗ ΕΝΕΡΓΕΙΑ ΑΠΟ ΣΤΑΘΕΡΗ ΔΥΝΑΜΗ ΣΕ ΜΙΑ Α.Α.Τ.
Ετικέτες
1. ΤΑΛΑΝΤΩΣΕΙΣ
,
1.1 Μηχανικές
,
1.1.δ Προβλήματα
Πέμπτη 6 Σεπτεμβρίου 2012
ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΟΜΟΓΕΝΩΝ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 2012
ΟΙ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΩΝ ΟΜΟΓΕΝΩΝ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 2012
Κυριακή 2 Σεπτεμβρίου 2012
Α.Α.Τ ΣΥΣΤΗΜΑΤΟΣ “ΚΑΤΑΚΟΡΥΦΟ ΕΛΑΤΗΡΙΟ – ΜΑΖΑ” ΜΕΡΟΣ 4ο - ΑΣΚΗΣΕΙΣ
Διαγράμματα και συναρτήσεις Uελ – x, Uελ – t,
σε σύστημα κατακόρυφο ελατήριο – μάζα
δυσκολεύουν τους μαθητές. Γι αυτό σκέφτηκα τα τρία πρώτα μέρη της τελευταίας, σχετικής
με το θέμα εργασίας, να τα συνοδεύσω με
ένα τέταρτο μέρος που να
περιλαμβάνει δύο εφαρμογές. Είναι δύο
ασκήσεις με δυσκολία λίγο πάνω του
μετρίου, που η λύση τους θα ωφελήσει, κατά τη γνώμη μου, πολύ τους αγαπητούς
μαθητές μας.
Αργότερα, θα ακολουθήσουν
ασκήσεις όπου θα ζητούνται οι συναρτήσεις Fελ – x, Fελ – t
1. Όλες οι δυναμικές ενέργειες μαζί
Ένα σώμα μάζας m= 2 kgr είναι στερεωμένο στο κάτω άκρο ενός κατακόρυφου ελατηρίου του οποίου το πάνω άκρο συγκρατείται από ακλόνητο στήριγμα. Ανεβάζουμε το σώμα μέχρι μια θέση Β πάνω από τη θέση ισορροπίας του και κάποια στιγμή το αφήνουμε ελεύθερο. Έτσι αρχίζει να εκτελεί α.α.τ., στη διάρκεια της οποίας η δυναμική ενέργεια του ελατηρίου, Uελ, μεταβάλλεται μεταξύ των τιμών 0 και 4 J, ενώ η παραμόρφωσή του μεταξύ των τιμών 0 και 0,2 m, όπως φαίνεται στο διάγραμμα.
Α. Πόσο είναι το πλάτος, η ενέργεια και η γωνιακή
συχνότητα της ταλάντωσης;
Β. Σε ποια θέση είναι Uελ = Uταλ;
Αν το επίπεδο μηδενικής βαρυτικής
δυναμικής ενέργειας διέρχεται από τη θέση αυτή, να δείξετε ότι για οποιαδήποτε
απομάκρυνση x του
σώματος από τη θέση ισορροπίας ισχύει:
Uελατ
+ Uβαρ = Uταλ = (1/2)kx2
Γ. Να γίνουν τα διαγράμματα Uταλ - x
και Κ – x
σε κοινό σύστημα ορθογωνίων αξόνων ενέργειας – απομάκρυνσης και να υπολογιστούν
οι ρυθμοί μεταβολής των ενεργειών αυτών τη στιγμή που το σώμα διέρχεται από τη
θέση όπου Uταλ
= Κ
κινούμενο πάνω από τη θέση ισορροπίας και κατευθυνόμενο προς την πάνω ακραία
θέση Β.
Δ. Αν ως χρονική στιγμή t = 0 θεωρήσουμε κάποια
στιγμή που το σώμα διέρχεται από τη θέση όπου η δυναμική ενέργεια του ελατηρίου
(Uελ) είναι ίση με την
ενέργεια της ταλάντωσης (Εταλ) και ελαττώνεται, να εξάγετε την εξίσωση
απομάκρυνσης – χρόνου (x-t).
Δίνεται: g = 10 m/s2
Ετικέτες
1. ΤΑΛΑΝΤΩΣΕΙΣ
,
1.1 Μηχανικές
,
1.1.δ Προβλήματα
2. Από την παραμόρφωση ελατηρίου στην απομάκρυνση ταλάντωσης κι
αντίστροφα. Μια άσκηση για εξάσκηση.
Το κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου είναι στερεωμένο σε οριζόντιο βάθρο ενώ στο πάνω άκρο του είναι δεμένο ένα σώμα που εκτελεί απλή αρμονική ταλάντωση με θετική φορά προς τα πάνω. Στο διάγραμμα βλέπουμε πώς μεταβάλλεται η δυναμική ενέργεια ελαστικότητας του ελατηρίου σε συνάρτηση με την απομάκρυνση του σώματος από τη θέση ισορροπίας του.
Το κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου είναι στερεωμένο σε οριζόντιο βάθρο ενώ στο πάνω άκρο του είναι δεμένο ένα σώμα που εκτελεί απλή αρμονική ταλάντωση με θετική φορά προς τα πάνω. Στο διάγραμμα βλέπουμε πώς μεταβάλλεται η δυναμική ενέργεια ελαστικότητας του ελατηρίου σε συνάρτηση με την απομάκρυνση του σώματος από τη θέση ισορροπίας του.
Α.
Να βρείτε τη σταθερά του ελατηρίου και την περίοδο της ταλάντωσης.
Β. Με τι ρυθμό μεταβάλλεται η δυναμική ενέργεια, λόγω
παραμόρφωσης, του ελατηρίου τη στιγμή που το σώμα διέρχεται από τη θέση
ισορροπίας του κινούμενο προς τα θετικά;
Γ. Αν τη χρονική στιγμή t = 0 η δυναμική ενέργεια του ελατηρίου είναι ίση με τη μέγιστη
κινητική ενέργεια του σώματος και αυξάνεται, ποια είναι η σχέση της
παραμόρφωσης του ελατηρίου σε συνάρτηση με το χρόνο;
Δίνεται: g =
10 m/sec2.
Ετικέτες
1. ΤΑΛΑΝΤΩΣΕΙΣ
,
1.1 Μηχανικές
,
1.1.δ Προβλήματα
Τετάρτη 18 Ιουλίου 2012
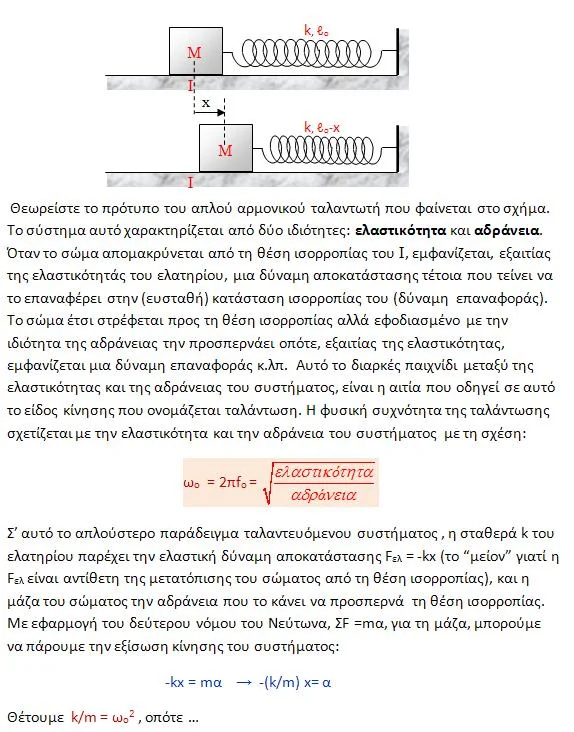
Το πρότυπο του απλού αρμονικού ταλαντωτή
Ετικέτες
1. ΤΑΛΑΝΤΩΣΕΙΣ
,
1.1 Μηχανικές
,
1.1.α Θέμα Α
,
1.1.β Θέμα Β
,
1.6 Θεωρητικά σημειώματα
Εγγραφή σε:
Αναρτήσεις
(
Atom
)