Όταν
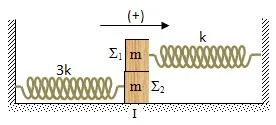
το σύστημα που φαίνεται στο σχήμα βρίσκεται σε ισορροπία, το δεξί ελατήριο είναι τεντωμένο κατά x1. Ο συντελεστής μέγιστης στατικής τριβής μεταξύ των
επιφανειών επαφής των δύο σωμάτων είναι μs, ενώ
δεν υπάρχει τριβή μεταξύ του κάτω σώματος και του δαπέδου. Όπως φαίνεται στο
σχήμα, οι σταθερές του δεξιού και του αριστερού ελατηρίου είναι k και 3k,
αντίστοιχα. Τα σώματα έχουν ίσες μάζες m.
Να βρείτε το μέγιστο πλάτος ταλάντωσης του συστήματος για το οποίο το πάνω σώμα δεν ολισθαίνει ως προς το κάτω.
Δείτε:
Να βρείτε το μέγιστο πλάτος ταλάντωσης του συστήματος για το οποίο το πάνω σώμα δεν ολισθαίνει ως προς το κάτω.
Δείτε:
Άλλη μια άσκηση με α.α.τ. και τριβή, που μπορεί να ξυπνά σε ορισμένους συναδέλφους και ιδιαίτερα στους μαθητές «που τολμούν να ξαναδοκιμάσουν» κακές αναμνήσεις από τις τελευταίες Πανελλήνιες, παρουσιάζει όμως ιδιαίτερο ενδιαφέρον κυρίως στην απλότητα της μεθόδου προσδιορισμού της μέγιστης τιμής του πλάτους με δεδομένο συντελεστή μs, ή, αντίστροφα, με δεδομένο το πλάτος, τον προσδιορισμό του συντελεστή μs.
ΑπάντησηΔιαγραφήΠροσέξτε επίσης τον τρόπο με τον οποίο μπορούμε να προσδιορίσουμε τη ΣF σε μια τυχαία θέση του ταλαντούμενου σώματος, χωρίς να κάνουμε χρήση της μαθηματικής σχέσης της συνθήκης ισορροπίας.
Η παραπάνω άσκηση είναι μια συνεισφορά του Eugene P. Mosca, U.S. Naval Academy, Annapolis στο περιοδικό Προκλήσεις Φυσικής για Δάσκαλους και μαθητές (Physics Challenges for Teachers and students)
ΑπάντησηΔιαγραφή