ΚΥΚΛΩΜΑ L-C - ΑΣΚΗΣΗ 1η

ΠΟΣΟ ΦΟΡΤΙΟ ΔΙΕΡΧΕΤΑΙ ΑΠΟ ΤΟ ΠΗΝΙΟ;

 

Στο κύκλωμα του διπλανού σχήματος είναι Ε = 10 V, r = 0 Ω, C = 16 μF και L = 1 Η, R₁ =  R₂ = 5 Ω.

Αρχικά ο διακόπτης είναι κλειστός και τα ρεύματα έχουν σταθεροποιηθεί. Τη χρονική στιγμή t = 0 τον ανοίγουμε και ακολουθεί ηλεκτρική ταλάντωση του κυκλώματος L-C.

α.  Να γραφούν οι εξισώσεις του ηλεκτρικού φορτίου του κάτω οπλισμού  …

Δείτε:

• Ολόκληρη την άσκηση
• Τη λύση της.

Τρείς ερωτήσεις στις ηλεκτρικές ταλαντώσεις ζητούν απάντηση:

3.  Ιδανικό κύκλωμα LC εκτελεί ηλεκτρική ταλάντωση με πλάτος έντασης ρεύματος 0,2 Α. Στο κύκλωμα έχουμε τη δυνατότητα να μεταβάλλουμε το συντελεστή αυτεπαγωγής L του πηνίου μετακινώντας τον πυρήνα μαλακού σιδήρου που υπάρχει σ' αυτό. Κάποια στιγμή που το φορτίο του πυκνωτή είναι μέγιστο ανοίγουμε το διακόπτη, μειώνουμε το συντελεστή αυτεπαγωγής του πηνίου σε L/4, και στη συνέχεια κλείνουμε πάλι το διακόπτη. Το πλάτος της έντασης του ρεύματος θα γίνει:

α. 0,1 Α,    β. 0,2 Α     γ. 0,3 Α      δ. 0,4 Α.

Α. Σημειώστε τη σωστή απάντηση.

Β. Να δικαιολογήσετε την απάντησή σας.

·         Όλες οι ερωτήσεις μαζί.

·         Οι απαντήσεις.

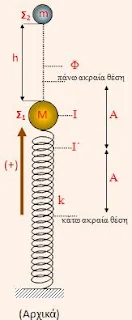
ΠΕΡΙΠΤΩΣΗ: ΒΟΛΗ ΠΡΟΣ ΤΑ ΠΑΝΩ – ΠΛΑΣΤΙΚΗ ΚΡΟΥΣΗ – Α.Α.Τ.

   ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΣΧΕΣΗΣ  x-t. ΑΛΛΗ ΜΙΑ ΣΧΕΣΗ “ΕΡΓΑΛΕΙΟ”

(Για λόγους απλότητας, προκειμένου να καταδειχτούν τα πολλά κοινά σημεία που έχει η περίπτωση αυτή με την περίπτωση της προηγούμενης ανάρτησης, θα προσεγγίσουμε και αυτό το θέμα  με τον ίδιο τρόπο ανάλυσης).

Και σε αυτήν την περίπτωση, επειδή το βάρος του συσσωματώματος είναι μεγαλύτερο από αυτό του ενός σώματος, η θέση ισορροπίας ( Ι΄)  της ταλάντωσης του συσσωματώματος  είναι χαμηλότερα από τη θέση ισορροπίας (Ι) του σώματος που αρχικά ισορροπεί μόνο του στο ελατήριο. Επίσης κι εδώ, η απόσταση ΙΊ αντιστοιχεί στην αρχική απομάκρυνση της ταλάντωσης.

Και εδώ, αν θεωρήσουμε πάλι την προς τα πάνω φορά θετική, η ταλάντωση αρχίζει από μια θέση ,τη Ι, με θετική απομάκρυνση (ίση με ΙΊ). Όμως τώρα η αρχική ταχύτητα είναι θετική (προς τα πάνω)  κι όχι αρνητική όπως πριν. Αυτό σημαίνει ότι, η αρχική φάση της ταλάντωσης θα περιορίζεται ανάμεσα στις τιμές 0 και π/2.

Αν βάλλουμε πάλι έναν από τους παρακάτω περιορισμούς:

Συνέχεια …

ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ – ΠΛΑΣΤΙΚΗ ΚΡΟΥΣΗ – Α.Α.Τ., ΜΙΑ ΣΧΕΣΗ “ΕΡΓΑΛΕΙΟ” ΓΙΑ ΤΗ ΣΥΝΑΡΤΗΣΗ x –t. (6ο θεωρητικό σημείωμα)

ΜΕΡΟΣ 1ο

Σε αυτές τις περιπτώσεις, ως γνωστόν, η θέση ισορροπίας ( Ι΄)  της ταλάντωσης του συσσωματώματος  είναι χαμηλότερα από τη θέση ισορροπίας (Ι) του σώματος που αρχικά ισορροπεί μόνο του στο ελατήριο. Επιπλέον, η απόσταση ΙΊ αντιστοιχεί στην αρχική απομάκρυνση x_αρχ της ταλάντωσης.

Έτσι, αν θεωρήσουμε την προς τα πάνω φορά θετική, στη θέση Ι, από την οποία αρχίζει την ταλάντωσή του το συσσωμάτωμα, αντιστοιχεί θετική απομάκρυνση x_αρχ (ίση με ΙΊ) κι αρνητική ταχύτητα (προς τα κάτω). Αυτό σημαίνει ότι, η αρχική φάση της ταλάντωσης θα περιορίζεται ανάμεσα στις τιμές π/2 και π.

Συνέχεια ...

                                                                                    
                                                          ΜΕΡΟΣ 2ο

Τι θα λέγατε τώρα αν σας καλούσαν να αντιμετωπίσετε αντίστροφα μια τέτοια περίπτωση, ελεύθερης πτώσης- πλαστικής κρούσης - α.α.τ. με φ₀ = 5π/6;

 Να σας έδιναν δηλαδή:

α) Την εξίσωση ταλάντωσης του συσσωματώματος και μόνο τη μια μάζα και να  σας ζητούσαν τα υπόλοιπα τρία μεγέθη, δηλαδή την άλλη μάζα, τη σταθερά k και το ύψος h,  ή

β) Την εξίσωση ταλάντωσης του συσσωματώματος και μόνο τη σταθερά k και να  σας ζητούσαν τα υπόλοιπα τρία μεγέθη: m, M και h.

(Στα δεδομένα, φυσικά, πρέπει να  ενταχθεί και τη σταθερά g).

Συνέχεια ...

Α.Α.Τ., ΤΟ TEST ΤΩΝ ΔΕΚΑ ΣΧΕΣΕΩΝ (Διάρκεια 2 h)

1. Ένα υλικό σημείο εκτελεί α.α.τ., τέτοια ώστε σε δύο θέσεις x₁ και x₂ να έχει ταχύτητες υ και u και επιταχύνσεις α και β, αντίστοιχα. Δείξτε ότι η απόσταση ανάμεσα στις θέσεις αυτές είναι:

Δείτε:

Όλο το test

Τις απαντήσεις

Εισαγωγικές εξετάσεις ομογενών στη Φυσική καταύθυνσης 2011

ΟΙ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΩΝ ΟΜΟΓΕΝΩΝ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 2011

• ΤΑ ΘΕΜΑΤΑ
• ΟΙ ΑΠΑΝΤΗΣΕΙΣ
• ΣΧΟΛΙΑ

1ο ΤΡΙΩΡΟ ΔΙΑΓΩΝΙΣΜΑ στις Απλές μηχανικές αρμονικές ταλαντώσεις

[Eξάσκηση στη χρήση των εξισώσεων των απλών αρμονικών ταλαντώσεων]

 (Τα πρώτα έξη από τα δέκα θέματα, που καλείστε παρακάτω να απαντήσετε, έχουν τη δυσκολία που συναντάμε στην κατηγορία “ΘΕΜΑ Β” των πανελληνίων. Τα υπόλοιπα τέσσερα μπορούν να θεωρηθούν ασκήσεις της κατηγορίας  “ΘΕΜΑ Γ”)

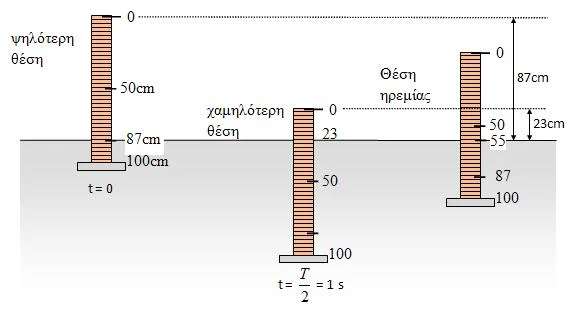
 Ένα απλό μοντέλο πυκνομέτρου (οργάνου μέτρησης της πυκνότητας των υγρών) μπορεί να κατασκευαστεί με τη βοήθεια ενός αριθμημένου ξύλινου χάρακα που στο ένα άκρο του έχουμε στερεώσει ένα μικρό βάρος. Έτσι ο χάρακας θα στέκεται κατακόρυφος όταν βυθίζεται μέσα σε ένα υγρό. Μετρώντας το βάθος όπου ισορροπεί ο χάρακας μπορούμε να έχουμε μια εκτίμηση για την πυκνότητα του υγρού.

Στο σχήμα φαίνονται οι ακραίες θέσεις μιας ταλάντωσης που κάνει ένα τέτοιο υδρόμετρο και η θέση ηρεμίας.

A. Το πλάτος της ταλάντωσης είναι:

α. 5 mm,    β. 17 mm,     γ. 32 mm,    δ. 37 mm

B. Το μέτρο της μέγιστης ταχύτητας είναι:

α. 0,032π m/s,  β. 0,017π m/s,  γ. 0.005π m/s,  δ. 0,037π m/s  

 Δείτε:

•  Ολόκληρο το διαγώνισμα
• Τις αναλυτικές απαντήσεις