Οι σταθερές των δύο
ελατηρίων του σχήματος είναι k1=
100 N/m και k2
= 300 N/m, ενώ οι μάζες των σωμάτων Σ1
και Σ2 είναι m1
= 1 kgr
και m2
= 3 kgr,
αντίστοιχα.
Οι σταθερές των δύο
ελατηρίων του σχήματος είναι k1=
100 N/m και k2
= 300 N/m, ενώ οι μάζες των σωμάτων Σ1
και Σ2 είναι m1
= 1 kgr
και m2
= 3 kgr,
αντίστοιχα.Στο χώρο αυτό, οι μαθητές της Γ Λυκείου αλλά και οι συνάδελφοι εκπαιδευτικοί θα βρουν μια σειρά από ερωτήσεις, πρωτότυπες ασκήσεις και προβλήματα στο πνεύμα των πανελλαδικών εξετάσεων. Το υλικό δημιουργήθηκε μέσα από χρόνια δουλειάς με μαθητές και συναδέλφους. μπορεί όμως ακόμη να έχει κάποιες ατέλειες. Κάθε καλοπροαίρετη παρατήρηση ή διόρθωση δεν είναι τυπικό σχόλιο· είναι μια μικρή, ουσιαστική συμβολή σε μια δουλειά που εξακολουθεί να εξελίσσεται μαζί σας.
Header's Buttons
Η φύση αγαπά την αλήθεια, και η αλήθεια της φύσης διεκδικεί το δικαίωμα να εκτίθεται μόνο σε όσους την ποθούν. (Φ. Ντοστογιέφσκι)
- ΤΡΑΠ.ΘΕΜ.Β ΛΥΚ
- Διεθνής Πύλη Προετοιμασίας για Ανώτατες Σπουδές
- Αρχική σελίδα
- Educational Videos & Interviews
- Richard Feynman
- Quantum Mechanics
- Tree-Hour Test 2
- Three-hour test 1
- Three-Hours Test 3
- Greek National Physics Exams — Problems & Solutions — 2002–2025
- Greek National Physics Exams — Problems & Solutions — 2002–2025
- Three-hour Tests
- High School 1st Year Exam Questions Bank
- Physics B' Lyceum: Strategic Question Bank for Greek University Entrance Exams
- Physics C' Lyceum: Strategic Question Bank for Greek University Entrance Exams
- Physics National Exams Simulations
- Federation of Greek Teachers
- Keystone We are in
- General Education Physics exams— Problems & Solutions (2000 - 2016)
- OEFE and Keystone simulation exams
- Physics Exam Preparation Portal
Παρασκευή 11 Μαΐου 2012
 Οι σταθερές των δύο
ελατηρίων του σχήματος είναι k1=
100 N/m και k2
= 300 N/m, ενώ οι μάζες των σωμάτων Σ1
και Σ2 είναι m1
= 1 kgr
και m2
= 3 kgr,
αντίστοιχα.
Οι σταθερές των δύο
ελατηρίων του σχήματος είναι k1=
100 N/m και k2
= 300 N/m, ενώ οι μάζες των σωμάτων Σ1
και Σ2 είναι m1
= 1 kgr
και m2
= 3 kgr,
αντίστοιχα.Σάββατο 5 Μαΐου 2012
ΤΑΛΑΝΤΩΣΗ ΣΤΗΝ ΚΑΤΑΚΟΡΥΦΗ ΔΙΕΥΘΥΝΣΗ ΚΑΙ ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ
Το πάνω άκρο ενός
κατακόρυφου ελατηρίου έχει στερεωθεί στην οροφή ενός δωματίου, ενώ στο κάτω
άκρο του έχει προσδεθεί σφαιρικό σώμα Σ1 μάζας m.
Υποβαστάζουμε
το σώμα ώστε το ελατήριο να έχει το φυσικό του μήκος ℓ0, και κάποια
στιγμή το αφήνουμε ελεύθερο. Το σώμα Σ1 αρχίζει να εκτελεί απλή
αρμονική ταλάντωση. Παρατηρούμε ότι το χαμηλότερο σημείο στο οποίο φτάνει,
απέχει από το σημείο που το αφήσαμε 20 cm.
Α. Υπολογίστε
τη συχνότητα της ταλάντωσης και το μέτρο της ταχύτητας του σώματος όταν περνάει
από τη θέση που βρίσκεται 10 cm πιο κάτω από τη θέση που το αφήσαμε.
Δίνεται: g = 10 m/sec2.
Β. Κάτω από το Σ1 και
σε απόσταση h = 50 cm από τη θέση που το αφήνουμε ελεύθερο
να ταλαντωθεί, βρίσκεται ένα άλλο σφαιρικό σώμα Σ2 ίδιας
μάζας με το Σ1. Το κέντρο του Σ2 βρίσκεται πάνω στην
κατακόρυφο που ταλαντώνεται το κέντρο του Σ1. Κάποια στιγμή το Σ2 βάλλεται
προς τα πάνω με αρχική ταχύτητα υ0 = 3 m/sec και
συγκρούεται κεντρικά κι ελαστικά με το Σ1. Σε ποια θέση πρέπει να
βρίσκεται το Σ1 τη στιγμή της κρούσης, ώστε μετά από αυτή, το
πλάτος της ταλάντωσής του να είναι το μέγιστο δυνατό; Δικαιολογείστε την
απάντησή σας.
Γ. Πόσο είναι ....
Πέμπτη 3 Μαΐου 2012
ΑΝΕΒΑΙΝΕΙ Ή ΚΑΤΕΒΑΙΝΕΙ;
..........................................................................................................................
Δείτε:
Τετάρτη 25 Απριλίου 2012
ΜΗ ΚΕΝΤΡΙΚΗ ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ
 Β. Πάνω σε ένα λείο οριζόντιο τραπέζι
ηρεμεί ένα σφαιρίδιο Σ2 μάζας m = 1 kgr
στερεωμένο στην άκρη οριζόντιου ελατηρίου σταθεράς k = 100 N/m, του οποίου το άλλο άκρο συγκρατείται από ακλόνητο στήριγμα.
Ένα δεύτερο σφαιρίδιο Σ1 ίδιας μάζας με το Σ2 κινείται με
ταχύτητα υ1 = √ 2 m/sec πάνω σε μια ευθεία που δε
διέρχεται από το κέντρο του Σ2 και σχηματίζει γωνία φ = 1350
με τον άξονα του ελατηρίου. Ακολουθεί
πλάγια ελαστική κρούση στο τέλος της οποίας διαπιστώνεται ότι το Σ2
κινείται κατά μήκος του άξονα του ελατηρίου κάνοντας απλή αρμονική ταλάντωση.
Β. Πάνω σε ένα λείο οριζόντιο τραπέζι
ηρεμεί ένα σφαιρίδιο Σ2 μάζας m = 1 kgr
στερεωμένο στην άκρη οριζόντιου ελατηρίου σταθεράς k = 100 N/m, του οποίου το άλλο άκρο συγκρατείται από ακλόνητο στήριγμα.
Ένα δεύτερο σφαιρίδιο Σ1 ίδιας μάζας με το Σ2 κινείται με
ταχύτητα υ1 = √ 2 m/sec πάνω σε μια ευθεία που δε
διέρχεται από το κέντρο του Σ2 και σχηματίζει γωνία φ = 1350
με τον άξονα του ελατηρίου. Ακολουθεί
πλάγια ελαστική κρούση στο τέλος της οποίας διαπιστώνεται ότι το Σ2
κινείται κατά μήκος του άξονα του ελατηρίου κάνοντας απλή αρμονική ταλάντωση.Δείτε:
Δευτέρα 23 Απριλίου 2012
Το «ταυ».
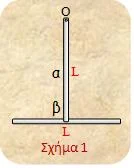 Ένα
εκκρεμές (σχήμα 1) αποτελείται από δύο παρόμοιες ομογενείς λεπτές ράβδους α και
β, με ίδιο μήκος L
= 0,6 m
και ίδια μάζα m
= 2/3 kgr,
συγκολλημένες κάθετα μεταξύ τους έτσι ώστε το ένα άκρο της α να συμπίπτει με το μέσον της β. Με τον τρόπο αυτό σχηματίζουν
ένα Τ το οποίο μπορεί να περιστρέφεται
γύρω από οριζόντιο άξονα, που διέρχεται από το άλλο άκρο Ο της α και είναι κάθετος στο επίπεδο
που ορίζεται από τις ράβδους. Έτσι, το «Τ» συμπεριφέρεται ως εκκρεμές που μπορεί να ταλαντώνεται πάνω στο κατακόρυφο επίπεδο που ορίζεται από
αυτό.
Ένα
εκκρεμές (σχήμα 1) αποτελείται από δύο παρόμοιες ομογενείς λεπτές ράβδους α και
β, με ίδιο μήκος L
= 0,6 m
και ίδια μάζα m
= 2/3 kgr,
συγκολλημένες κάθετα μεταξύ τους έτσι ώστε το ένα άκρο της α να συμπίπτει με το μέσον της β. Με τον τρόπο αυτό σχηματίζουν
ένα Τ το οποίο μπορεί να περιστρέφεται
γύρω από οριζόντιο άξονα, που διέρχεται από το άλλο άκρο Ο της α και είναι κάθετος στο επίπεδο
που ορίζεται από τις ράβδους. Έτσι, το «Τ» συμπεριφέρεται ως εκκρεμές που μπορεί να ταλαντώνεται πάνω στο κατακόρυφο επίπεδο που ορίζεται από
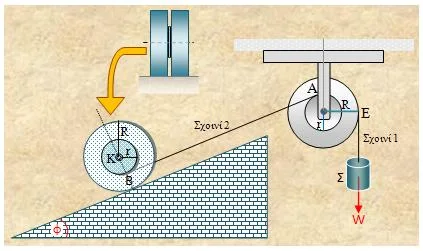
αυτό. Β.
Στο σχήμα 2, το «Τ» ισορροπεί μαζί με ένα στερεό, το οποίο αποτελείται από δύο
ομόκεντρες, κολλημένες μεταξύ τους, ομογενείς τροχαλίες. Η κοινή ισορροπία
επιτυγχάνεται με τη βοήθεια δύο κατακόρυφων λεπτών σχοινιών που είναι τυλιγμένα
στα αυλάκια των τροχαλιών του στερεού. H ακτίνα R της μεγάλης τροχαλίας είναι 0,2 m, ενώ της μικρής είναι r = 0,1 m.
Β.
Στο σχήμα 2, το «Τ» ισορροπεί μαζί με ένα στερεό, το οποίο αποτελείται από δύο
ομόκεντρες, κολλημένες μεταξύ τους, ομογενείς τροχαλίες. Η κοινή ισορροπία
επιτυγχάνεται με τη βοήθεια δύο κατακόρυφων λεπτών σχοινιών που είναι τυλιγμένα
στα αυλάκια των τροχαλιών του στερεού. H ακτίνα R της μεγάλης τροχαλίας είναι 0,2 m, ενώ της μικρής είναι r = 0,1 m.