ΠΡΙΣΜΑ ΜΕ ΤΟΜΗ ΟΡΘΟΓΩΝΙΟΥ ΤΡΙΓΩΝΟΥ ΣΤΟ ΝΕΡΟ ΚΑΙ ΜΙΑ ΠΑΡΑΤΗΡΗΣΗ

Μια παραλλαγή της 2.44 σελ. 83 του σχολικού βιβλίου.

 Ένα γυάλινο πρίσμα με τομή σχήματος ορθογωνίου τριγώνου είναι βυθισμένο εν μέρει μέσα στο νερό όπως στο σχήμα. Μια ακτίνα μονοχρωματικού φωτός προσπίπτει κάθετα στην πλευρά ΑΒ προερχόμενη από τον αέρα

Δείτε:

Ολόκληρη την ερώτηση

Την απάντηση

ΚΥΜΑΤΙΚΟΣ ΠΑΛΜΟΣ

Ένας κυματικός παλμός … από την Αντιγόνη

Την παρακάτω άσκηση  τη φτιάξαμε μαζί με τη μαθήτριά μου Αντιγόνη. Όλα ξεκίνησαν όταν εξέφρασε την απορία:

« Και τι γίνεται όταν η πηγή αρμονικής διαταραχής σταματήσει να ταλαντώνεται;»

Την αφιερώνουμε σε όλους  τους αναγνώστες .

Το άκρο Ο ενός γραμμικού ομογενούς ελαστικού μέσου που εκτείνεται κατά τη διεύθυνση του ημιάξονα Οx αρχίζει, τη στιγμή t = 0, να ταλαντώνεται σύμφωνα με την εξίσωση  ψ = 0,2ημ2πt  (S.I).  Η ταλάντωση του υλικού σημείου Ο διαδίδεται στο μέσο με ταχύτητα υ = 5 m/sec. Τη στιγμή t₁ = 2,5 sec διακόπτεται η ταλάντωσή του...

ΑΝΑΚΛΑΣΗ – ΔΙΑΘΛΑΣΗ – ΝΟΜΟΣ ΤΟΥ Snell – ΘΕΜΑ Β. Ερώτηση 1η

1. Γωνία εκτροπής σε ένα γυάλινο τριγωνικό πρίσμα.

Το γυάλινο τριγωνικό πρίσμα που φαίνεται στην εικόνα έχει δείκτη διάθλασης  n_γ  = √ 3 

Ο αέρας γύρω του έχει δείκτη n_α = 1.  

Για την περίπτωση που φαίνεται στο σχήμα,  να υπολογίσετε τη γωνία εκτροπής ε της φωτεινής ακτίνας.

·        ΑΠΑΝΤΗΣΗ

ΑΝΑΚΛΑΣΗ – ΔΙΑΘΛΑΣΗ – ΝΟΜΟΣ ΤΟΥ Snell – ΘΕΜΑ Β. Ερώτηση 2η

2. Φαινόμενο βάθος = Πραγματικό βάθος/n. Πότε ισχύει.

  Όπως φαίνεται στο σχήμα, ένα αντικείμενο Σ είναι σε βάθος Η μέσα σε ένα  διάφανο υγρό με δείκτη διάθλασης n. Σε πόσο βάθος βλέπουμε το αντικείμενο καθώς το κοιτάζουμε από ένα σημείο που βρίσκεται πάνω στην κατακόρυφο Σψ ή σχεδόν πάνω σ’ αυτήν;

Δίνεται ότι για μικρές γωνίες η εφαπτομένη είναι περίπου ίση με το ημίτονο.

·        ΑΠΑΝΤΗΣΗ

ΑΝΑΚΛΑΣΗ – ΔΙΑΘΛΑΣΗ – ΝΟΜΟΣ ΤΟΥ Snell – ΘΕΜΑ Β. Ερώτηση 3η

3. Μια “καθολική” ολική εσωτερική ανάκλαση                                                       

Όπως φαίνεται στο σχήμα, μια ακτίνα προσπίπτει στην πλευρική επιφάνεια ενός γυάλινου παραλληλεπίπεδου πρίσματος απεριόριστου μήκους και εισέρχεται στο εσωτερικό του. Ο δείκτης διάθλασης του πρίσματος είναι n.

 Δείξτε ότι αν n >√ 2 , όλες οι εισερχόμενες ακτίνες μπορούν να υποστούν ολική εσωτερική ανάκλαση.

(Εξαιρείται φυσικά η περίπτωση όπου π₁ = 0^ο).

Απάντηση 

Δείτε επίσης:

•  ΑΝΑΚΛΑΣΗ – ΔΙΑΘΛΑΣΗ, ΠΕΝΤΕ ΕΥΚΟΛΑ ΚΟΜΜΑΤΙΑ ΘΕΜΑ Β
• ΤΙΣ ΑΠΑΝΤΗΣΕΙΣ

ΑΡΜΟΝΙΚΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ. ΜΙΑ ΠΟΛΥ ΒΑΣΙΚΗ ΑΣΚΗΣΗ

Στο στιγμιότυπο της στιγμής t₁ ενός αρμονικού κύματος, που διαδίδεται κατά μήκος μιας χορδής και περιγράφεται από την εξίσωση ψ = Αημ2π(t/T  - x/λ), η φάση μεταβάλλεται σε σχέση με την απόσταση από την αρχή αξόνων όπως δείχνει το διάγραμμα (α), ενώ η φάση της ταλάντωσης ενός υλικού σημείου Σ της χορδής σε συνάρτηση με το χρόνο μεταβάλλεται όπως στο διάγραμμα (β).

α)  Προσδιορίστε την απόσταση του υλικού σημείου Σ από την αρχή αξόνων καθώς και τη χρονική στιγμή t₁.

β)  Αν η μέγιστη επιτάχυνση των μορίων του ελαστικού μέσου διάδοσης είναι ...
Δείτε:

 

·         Ολόκληρη την άσκηση
·         Συνοπτική απάντηση

·         Αναλυτική απάντηση

2ο τρίωρο στις ταλαντώσεις (επαναληπτικο)

Ένα διαγώνισμα στο “πνεύμα” των εξετάσεων, δώρο από το … “πνεύμα” των Εορτών

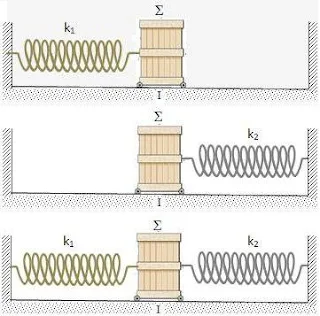
B.1. Αν το κιβώτιο του σχήματος συνδεθεί με το αριστερό ελατήριο σταθεράς k₁ και διεγερθεί κατάλληλα θα εκτελέσει  α.α.τ. με συχνότητα f₁. Όμοια, αν συνδεθεί με το δεξί ελατήριο σταθεράς k₂ θα εκτελέσει α.α.τ με συχνότητα f₂.

.

Δείξτε ότι αν συνδεθεί και με τα δύο ελατήρια όπως στο τρίτο σχήμα, και διεγερθεί κατάλληλα, θα κάνει α.α.τ. με συχνότητα f  για την οποία:

                                           f² = f₁² + f₂²

 (Δίνεται ότι όταν το κιβώτιο βρίσκεται στη θέση Ι τα δύο ελατήρια έχουν το φυσικό τους μήκος. Δίνεται, επίσης, ότι το κιβώτιο κινείται χωρίς τριβές στην οριζόντια επιφάνεια και ότι τα στηρίγματα δεξιά και αριστερά στα οποία στερεώνονται τα ελατήρια είναι σταθερά).

Δείτε:

·         Ολόκληρο το διαγώνισμα

·         Τι πρέπει να γνωρίζετε

·         Αναλυτική απάντηση
·         Πόσο εύκολο είναι …