Απάντηση σε word:
Παρατήρηση:
Στο χώρο αυτό, οι μαθητές της Γ Λυκείου αλλά και οι συνάδελφοι εκπαιδευτικοί θα βρουν μια σειρά από ερωτήσεις, πρωτότυπες ασκήσεις και προβλήματα στο πνεύμα των πανελλαδικών εξετάσεων. Το υλικό δημιουργήθηκε μέσα από χρόνια δουλειάς με μαθητές και συναδέλφους. μπορεί όμως ακόμη να έχει κάποιες ατέλειες. Κάθε καλοπροαίρετη παρατήρηση ή διόρθωση δεν είναι τυπικό σχόλιο· είναι μια μικρή, ουσιαστική συμβολή σε μια δουλειά που εξακολουθεί να εξελίσσεται μαζί σας.

Το σύστημα “ράβδος – σφαιρίδιο Σ1” του
σχήματος, μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από ακλόνητο οριζόντιο
άξονα, κάθετο στο άκρο Ο της ράβδου. Η μάζα του Σ1 είναι ίση με
τα 2/3 της μάζας Μ της ράβδου, ενώ του Σ2 είναι τετραπλάσια της
μάζας της ράβδου.
Αφήνουμε ελεύθερο το σύστημα από την οριζόντια θέση. Όταν φτάσει στην κατακόρυφη θέση συγκρούεται με το σφαιρίδιο Σ2 και ακινητοποιείται, ενώ το Σ2, δεμένο στην άκρη ενός σχοινιού μήκους L/2,, αρχίζει να εκτελεί κυκλική κίνηση σε κατακόρυφο επίπεδο, με κέντρο το ακλόνητο άλλο άκρο του σχοινιού.
α. Να εξετάσετε αν η κρούση είναι ελαστική.
β. Να δείξετε ότι το σφαιρίδιο Σ2 δεν
θα μπορέσει να εκτελέσει ανακύκλωση.
γ. Να προσδιορίσετε τη θέση όπου διακόπτεται η κυκλική
κίνηση.
δ. Να βρείτε τη γραμμική επιτάχυνση, τη γωνιακή
επιτάχυνση και το ρυθμό μεταβολής της στροφορμής του Σ2, στην
παραπάνω θέση.
Δίνονται: για τη ράβδο M = 1 kg,
Ιcm = (1/12)ML2 και το μήκος
της L = 2 m, καθώς και η επιτάχυνση
βαρύτητας g = 10 m/s2.
Να θεωρήσετε ότι (√119)/12 = 0,9.
Μια σφαίρα, μάζας m = 1 kg και
ακτίνας r = 0,1 m συγκρατείται αρχικά στη θέση που φαίνεται
στο σχήμα. Κάποια στιγμή αφήνεται ελεύθερη (χωρίς να την σπρώξουμε).
α. Η σφαίρα κυλίεται στο κοίλο ημισφαιρικό
δοχείο, ακτίνας R = 1,1 m, του σχήματος χωρίς να ολισθαίνει. Με
πόση ταχύτητα διέρχεται από το χαμηλότερο σημείο Β του δοχείου;
β. Αν στη συνέχεια (μετά το σημείο Β) η εσωτερική
επιφάνεια του δοχείου είναι λεία, να εξετάσετε, χωρίς υπολογισμούς:
i. αν η σφαίρα θα φτάσει (κινούμενη στο
λείο τμήμα του δοχείου) σε ύψος ίσο με εκείνο από το οποίο ξεκίνησε,
ii. αν, μετά την επιστροφή της στο σημείο Β, η
σφαίρα θα επανέλθει στη θέση απ’ όπου την αφήσαμε.
Δίνεται η ροπή αδράνειας της σφαίρας Ιcm =
4·10-3 kg·m2 και η επιτάχυνση
βαρύτητας g = 10 m/s2.
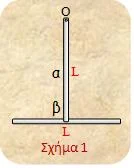 Ένα
εκκρεμές (σχήμα 1) αποτελείται από δύο παρόμοιες ομογενείς λεπτές ράβδους α και
β, με ίδιο μήκος L
= 0,6 m
και ίδια μάζα m
= 2/3 kgr,
συγκολλημένες κάθετα μεταξύ τους έτσι ώστε το ένα άκρο της α να συμπίπτει με το μέσον της β. Με τον τρόπο αυτό σχηματίζουν
ένα Τ το οποίο μπορεί να περιστρέφεται
γύρω από οριζόντιο άξονα, που διέρχεται από το άλλο άκρο Ο της α και είναι κάθετος στο επίπεδο
που ορίζεται από τις ράβδους. Έτσι, το «Τ» συμπεριφέρεται ως εκκρεμές που μπορεί να ταλαντώνεται πάνω στο κατακόρυφο επίπεδο που ορίζεται από
αυτό.
Ένα
εκκρεμές (σχήμα 1) αποτελείται από δύο παρόμοιες ομογενείς λεπτές ράβδους α και
β, με ίδιο μήκος L
= 0,6 m
και ίδια μάζα m
= 2/3 kgr,
συγκολλημένες κάθετα μεταξύ τους έτσι ώστε το ένα άκρο της α να συμπίπτει με το μέσον της β. Με τον τρόπο αυτό σχηματίζουν
ένα Τ το οποίο μπορεί να περιστρέφεται
γύρω από οριζόντιο άξονα, που διέρχεται από το άλλο άκρο Ο της α και είναι κάθετος στο επίπεδο
που ορίζεται από τις ράβδους. Έτσι, το «Τ» συμπεριφέρεται ως εκκρεμές που μπορεί να ταλαντώνεται πάνω στο κατακόρυφο επίπεδο που ορίζεται από
αυτό. Β.
Στο σχήμα 2, το «Τ» ισορροπεί μαζί με ένα στερεό, το οποίο αποτελείται από δύο
ομόκεντρες, κολλημένες μεταξύ τους, ομογενείς τροχαλίες. Η κοινή ισορροπία
επιτυγχάνεται με τη βοήθεια δύο κατακόρυφων λεπτών σχοινιών που είναι τυλιγμένα
στα αυλάκια των τροχαλιών του στερεού. H ακτίνα R της μεγάλης τροχαλίας είναι 0,2 m, ενώ της μικρής είναι r = 0,1 m.
Β.
Στο σχήμα 2, το «Τ» ισορροπεί μαζί με ένα στερεό, το οποίο αποτελείται από δύο
ομόκεντρες, κολλημένες μεταξύ τους, ομογενείς τροχαλίες. Η κοινή ισορροπία
επιτυγχάνεται με τη βοήθεια δύο κατακόρυφων λεπτών σχοινιών που είναι τυλιγμένα
στα αυλάκια των τροχαλιών του στερεού. H ακτίνα R της μεγάλης τροχαλίας είναι 0,2 m, ενώ της μικρής είναι r = 0,1 m.