Γενικό διαγώνισμα στις μηχανικές ταλαντώσεις και στις κρούσεις

                                        (3^ωρο, για πολύ καλά προετοιμασμένους)

     [Το διαγώνισμα αυτό είναι δύσκολο όχι γιατί περιέχει εξεζητημένα θέματα, αλλά γιατί απαιτεί καλή  προετοιμασία ώστε να προλάβετε να απαντήσετε σε όλα τα θέματα μέσα στις τρεις ώρες.]

Αποσπάσματα:

Α1. Καθώς μειώνεται το πλάτος μιας φθίνουσας ταλάντωσης με δύναμη απόσβεσης της μορφής F_απ= -bυ:

α. Μειώνεται η περίοδος της ταλάντωσης

β. μειώνεται η ενέργεια που χάνεται σε κάθε περίοδο

γ. μειώνεται η σταθερά απόσβεσης b

δ. αυξάνεται ο ρυθμός μείωσης του πλάτους.

..........................................................................

Α4. Δύο σφαίρες συγκρούονται κεντρικά και ελαστικά. Επομένως:

α. μεγαλύτερο μέτρο έχει η μεταβολή της ορμής της σφαίρας με τη μικρότερη μάζα.

β. οι δύο σφαίρες έχουν ίδια μεταβολή στην ορμή τους.

γ. Η μεταβολή της κινητικής ενέργειας της σφαίρας με τη μεγαλύτερη μάζα είναι μικρότερη από τη μεταβολή της κινητικής ενέργειας της σφαίρας με τη μικρότερη μάζα.

δ. το αλγεβρικό άθροισμα των ταχυτήτων πριν και μετά την κρούση είναι το ίδιο για κάθε σφαίρα.

............................................................................

Β2. Ένα σώμα εκτελεί εξαναγκασμένη ταλάντωση και η απομάκρυνση του σώματος σε συνάρτηση με το χρόνο μεταβάλλεται σύμφωνα με την εξίσωση x = 0,3ημ10πt (S.Ι). Αν η συχνότητα του διεγέρτη αυξηθεί κατά 5 Ηz, η μέγιστη ταχύτητα ταλάντωσης διπλασιάζεται σε σχέση με την αρχική. Επομένως η συχνότητα συντονισμού f₀ του ταλαντωτή είναι:

                     α. f₀ < 5 Hz,        β. f₀  > 10 Hz,           γ. 5Hz < f₀ < 10 Hz

Επιλέξτε την ορθή ανισότητα και αιτιολογήσετε την επιλογή σας.

Δείτε όλο το διαγώνισμα εδώ

Αναλυτικές απαντήσεις εδώ

3ο ΤΡΙΩΡΟ (+) ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ (ΕΠΑΝΑΛΗΠΤΙΚΟ)

          Θέμα Α

 (Για καθεμιά από τις παρακάτω προτάσεις να γράψετε στο τετράδιό σας τον  αριθμό της αρχικής φράσης και, δίπλα, το γράμμα  ή τη σχέση που τη συμπληρώνει σωστά.).

 

Α.1.Στη διάταξη που φαίνεται στο διπλανό σχήμα, τα τρία σώματα Α, Β και Γ είναι κρεμασμένα μέσω ιδανικών ελατηρίων από την ίδια ράβδο. Ο κυκλικός δίσκος Δ μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα που περνάει από το κέντρο του. Αυξάνουμε αργά – αργά τη συχνότητα περιστροφής του δίσκου, ξεκινώντας από πολύ μικρές τιμές, κι έτσι η ράβδος Ρ εξαναγκάζεται να εκτελέσει α.α.τ., σταθερού πλάτους παραμένοντας διαρκώς οριζόντια. Αν m_A = m_B = m, m_Γ = 2m, και k_A = k_Γ = k,  k_B = 2k, με ποια σειρά θα αποκτήσουν μέγιστο πλάτος ταλάντωσης τα τρία σώματα;

α.    Α - Β - Γ,         β.    Γ - Β - Α, 

γ.    Β - Α - Γ,         δ.    Γ - Α - Β                                                                 

                                                                                      Μονάδες 5   

2ο τρίωρο στις ταλαντώσεις (επαναληπτικο)

Ένα διαγώνισμα στο “πνεύμα” των εξετάσεων, δώρο από το … “πνεύμα” των Εορτών

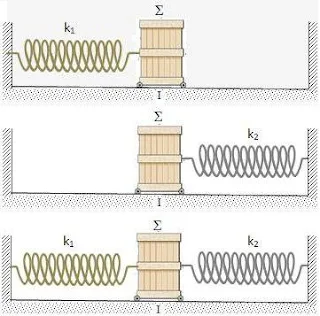
B.1. Αν το κιβώτιο του σχήματος συνδεθεί με το αριστερό ελατήριο σταθεράς k₁ και διεγερθεί κατάλληλα θα εκτελέσει  α.α.τ. με συχνότητα f₁. Όμοια, αν συνδεθεί με το δεξί ελατήριο σταθεράς k₂ θα εκτελέσει α.α.τ με συχνότητα f₂.

.

Δείξτε ότι αν συνδεθεί και με τα δύο ελατήρια όπως στο τρίτο σχήμα, και διεγερθεί κατάλληλα, θα κάνει α.α.τ. με συχνότητα f  για την οποία:

                                           f² = f₁² + f₂²

 (Δίνεται ότι όταν το κιβώτιο βρίσκεται στη θέση Ι τα δύο ελατήρια έχουν το φυσικό τους μήκος. Δίνεται, επίσης, ότι το κιβώτιο κινείται χωρίς τριβές στην οριζόντια επιφάνεια και ότι τα στηρίγματα δεξιά και αριστερά στα οποία στερεώνονται τα ελατήρια είναι σταθερά).

Δείτε:

·         Ολόκληρο το διαγώνισμα

·         Τι πρέπει να γνωρίζετε

·         Αναλυτική απάντηση
·         Πόσο εύκολο είναι …

1ο ΤΡΙΩΡΟ ΔΙΑΓΩΝΙΣΜΑ στις Απλές μηχανικές αρμονικές ταλαντώσεις

[Eξάσκηση στη χρήση των εξισώσεων των απλών αρμονικών ταλαντώσεων]

 (Τα πρώτα έξη από τα δέκα θέματα, που καλείστε παρακάτω να απαντήσετε, έχουν τη δυσκολία που συναντάμε στην κατηγορία “ΘΕΜΑ Β” των πανελληνίων. Τα υπόλοιπα τέσσερα μπορούν να θεωρηθούν ασκήσεις της κατηγορίας  “ΘΕΜΑ Γ”)

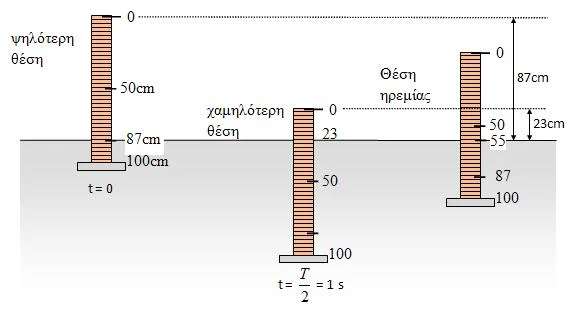
 Ένα απλό μοντέλο πυκνομέτρου (οργάνου μέτρησης της πυκνότητας των υγρών) μπορεί να κατασκευαστεί με τη βοήθεια ενός αριθμημένου ξύλινου χάρακα που στο ένα άκρο του έχουμε στερεώσει ένα μικρό βάρος. Έτσι ο χάρακας θα στέκεται κατακόρυφος όταν βυθίζεται μέσα σε ένα υγρό. Μετρώντας το βάθος όπου ισορροπεί ο χάρακας μπορούμε να έχουμε μια εκτίμηση για την πυκνότητα του υγρού.

Στο σχήμα φαίνονται οι ακραίες θέσεις μιας ταλάντωσης που κάνει ένα τέτοιο υδρόμετρο και η θέση ηρεμίας.

A. Το πλάτος της ταλάντωσης είναι:

α. 5 mm,    β. 17 mm,     γ. 32 mm,    δ. 37 mm

B. Το μέτρο της μέγιστης ταχύτητας είναι:

α. 0,032π m/s,  β. 0,017π m/s,  γ. 0.005π m/s,  δ. 0,037π m/s  

 Δείτε:

•  Ολόκληρο το διαγώνισμα
• Τις αναλυτικές απαντήσεις

ΔΥΟ Επαναληπτικά διαγωνίσματα στις απλές αρμονικές ταλαντώσεις

 1^ο Επαναληπτικό διαγώνισμα 40 min στις ταλαντώσεις.

   1. Το διάγραμμα του σχήματος παριστάνει την επιτάχυνση ενός σώματος, που εκτελεί α.α.τ, σε συνάρτηση με το χρόνο.

  Να χαρακτηρίσετε με Σ (αν είναι σωστή) ή με Λ (αν είναι λάθος) καθεμιά από τις παρακάτω προτάσεις.

α)  Στο σημείο Α αντιστοιχεί απομάκρυνση –Α,

β)  Στο σημείο Β του διαγράμματος η ταχύτητα είναι θετική,

γ)  Στο σημείο Γ η δύναμη επαναφοράς έχει μέγιστο μέτρο,

δ)  Στο σημείο Δ η απομάκρυνση είναι μέγιστη αρνητική,

ε)  Η ταχύτητα, στη διάρκεια που αντιστοιχεί μεταξύ των σημείων Γ και Δ, είναι θετική. 

Δείτε τα δύο διαγωνίσματα εδώ ...  και την αναλυτική απάντηση εδώ ...

ΔΙΩΡΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΦΘΙΝΟΥΣΕΣ ΚΑΙ ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

ΘΕΜΑ  Α

i) Ερωτήσεις πολλαπλής επιλογής.

(Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά).

Α1.  Η  αντιτιθέμενη δύναμη  F΄,  που  κάνει τη μέγιστη θετική απομάκρυνση  μιας  ταλάντωσης να  φθίνει εκθετικά με το χρόνο,  έχει πάντα φορά:

α)  ίδια με  τη φορά  της απομάκρυνσης του σώματος ,

β)  αντίθετη προς τη δύναμη  επαναφοράς της ταλάντωσης,

γ)  προς τις ακραίες θέσεις της ταλάντωσης,

δ)  αντίθετη προς τη φορά της ταχύτητας του  ταλαντωτή.

A2.   Σε μια φθίνουσα μηχανική ταλάντωση,  περιόδου Τ,  η μέγιστη  θετική απομάκρυνση μειώνεται με το χρόνο σύμφωνα με την εξίσωση: A  = A_ο e^-Λt.  Αν  τη χρονική στιγμή  t_α =  kΤ,  το πλάτος  της  ταλάντωσης είναι  Α_α ,  τότε τη χρονική στιγμή  t _β =  t _α + Τ,  το πλάτος της ταλάντωσης  θα  είναι: 

 α)  Α_α e^ΛT,             β)  Α_α e^-2ΛT,           γ)  Α_α e^2ΛT,                 δ)  Α_α e^-ΛT

Δίνεται ότι k = 1, 2, 3,...

Η συνέχεια εδώ ...  και η αναλυτική απάντηση εδώ ...

ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ - ΕΝΑ ΔΙΩΡΟ ΔΙΑΓΩΝΙΣΜΑ

ΘΕΜΑ  Α

i) Ερωτήσεις πολλαπλής επιλογής.

(Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά).

A1. Σ’ ένα κύκλωμα L – C που εκτελεί αμείωτη ηλεκτρική ταλάντωση, το φορτίο του πυκνωτή μεταβάλλεται σύμφωνα με τη σχέση  q = Qσυνωt :

α.  η μέγιστη ένταση του ηλεκτρικού ρεύματος είναι ω²Q.

β.  η μέγιστη τάση από αυτεπαγωγή στα άκρα του πηνίου είναι  Lω²Q.

γ.  ο μέγιστος ρυθμός μεταβολής της έντασης του ρεύματος στο κύκλωμα είναι ωQ.

δ.  η μέγιστη ηλεκτρική ενέργεια του πυκνωτή έχει τιμή  ½ Lω²Q.

Δείτε τη συνέχεια εδώ και τις απαντήσεις εδώ

ΔΙΩΡΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΑΠΛΕΣ ΑΡΜΟΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

A.    Ερωτήσεις

i)   Πολλαπλής επιλογής

(Για καθεμιά από τις παρακάτω προτάσεις να γράψετε στο τετράδιό σας τον  αριθμό της αρχικής φράσης και, δίπλα, το γράμμα  ή τη σχέση που τη συμπληρώνει σωστά.).

1.  Η επιτάχυνση ενός σώματος, που κάνει α.α.τ, μεταβάλλεται σε σχέση με την ταχύτητα σύμφωνα με το διάγραμμα:

                                                                                                                                 Μονάδες 10

2. Η απομάκρυνση x ενός απλού αρμονικού ταλαντωτή, σε συνάρτηση με το χρόνο, δίνεται από το πλαϊνό διάγραμμα. Η επιτάχυνση του σώματος και η ταχύτητά του έχουν αντίθετες κατευθύνσεις τη χρονική στιγμή που αντιστοιχεί:

 α.     στο σημείο Α.               β. στο σημείο Β.

 γ.     στο σημείο Γ.                δ. στο σημείο Δ. 

                                                                                                                             Μονάδες 10

Δείτε ολόκληρο το διαγώνισμα εδώ