Ελατήρια σώματα και "απώλεια επαφής"

Εφόσον υπάρχουν οι προϋποθέσεις για απώλεια επαφής σε ένα ταλαντούμενο σύστημα με ελατήριο, αυτή θα συμβεί τη στιγμή που το ελατήριο αποκτά το φυσικό του μήκος.

 

ΠΕΝΤΕ ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΟΡΙΖΟΝΤΙΟ ΕΛΑΤΗΡΙΟ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ

1. Όπου θα μας απασχολήσει η μέγιστη ισχύς της δύναμης ελατηρίου.

 Σώμα μάζας M = 1kgr βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και είναι προσδεμένο στην άκρη οριζόντιου ελατηρίου σταθεράς k = 100 Ν/m, η άλλη άκρη του οποίου είναι στερεωμένη ακλόνητα.

  Θέτουμε το σώμα σε α.α.τ. πλάτους  A₁ = 3,2 m.  Ένα βλήμα μάζας m = 0,21 kgr που κινείται στη διεύθυνση του άξονα του ελατηρίου με ταχύτητα υ = 100 m/sec, συγκρούεται πλαστικά με το σώμα, τη στιγμή που αυτό βρίσκεται  στη θέση ισορροπίας του, κινούμενο προς το βλήμα. Να υπολογίσετε:

2. Πλαστική κρούση με αύξηση της ενέργειας ταλάντωσης; Κι όμως γίνεται!

Σώμα μάζας M = 2,5 kgr βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και είναι προσδεμένο στην άκρη οριζόντιου ελατηρίου σταθεράς k = 100 Ν/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο τοίχο.

  Θέτουμε το σώμα σε α.α.τ. πλάτους 0,5 m.  Ένα βλήμα μάζας m = 0,5 kgr που κινείται στη διεύθυνση του άξονα του ελατηρίου με ταχύτητα υ = 30 m/sec, συγκρούεται με το σώμα, τη στιγμή που αυτό βρίσκεται  στην αρνητική ακραία θέση του, και σφηνώνεται σ’ αυτό. Να προσδιορίσετε:

α)  Την ενέργεια ...

Συνέχεια ...

3. Όπου το μέτρο του ρυθμού μεταβολής της δυναμικής ενέργειας του ελατηρίου είναι ζητούμενο

 Σώμα μάζας M₁ = 1 kgr βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και είναι προσδεμένο στην άκρη οριζόντιου ελατηρίου που έχει σταθερά k = 100 Ν/m και το άλλο του άκρο στερεωμένο ακλόνητα.
 Θέτουμε το σώμα αυτό σε α.α.τ. πλάτους Α₁ =√ 2 m.  Ένα άλλο σώμα μάζας Μ₂ = 2 kgr, που κινείται στη διεύθυνση του άξονα του ελατηρίου με ταχύτητα υ₂ = 20 m/sec, συγκρούεται πλαστικά με το πρώτο σώμα  στη θέση όπου η κινητική ενέργεια ταλάντωσης είναι ίση με το μισό της ενέργειας ταλάντωσης. Το συσσωμάτωμα, που δημιουργείται, ξεκινά μια νέα α.α.τ. με πλάτος Α₂. Η απομάκρυνση του Μ₁ στη θέση της σύγκρουσης είναι θετική και πριν τη σύγκρουση κινούνταν προς τη θετική ακραία θέση, αντίθετα από το Μ₂. Να προσδιορίσετε: 

Συνέχεια ...

4. Ρυθμός μεταβολής του μήκους του ελατηρίου και μηδενισμός της ισχύος της δύναμής του

 Πάνω σε ένα λείο οριζόντιο επίπεδο ηρεμεί αρχικά, δεμένο στο ένα άκρο ενός οριζόντιου ελατηρίου, σώμα μάζας M = 2 kgr. Το ελατήριο έχει σταθερά ελαστικότητας k = 200 Ν/m και η άλλη άκρη του είναι στερεωμένη ακλόνητα.

  Θέτουμε το σώμα αυτό σε α.α.τ. πλάτους Α₁ =√ 2 m. Ένα άλλο σώμα μάζας m = 0,25 kgr, που κινείται στη διεύθυνση του άξονα του ελατηρίου με ταχύτητα υ₂ = 80 m/sec, συγκρούεται πλαστικά με το πρώτο σώμα, τη στιγμή που αυτό βρίσκεται  στη θέση όπου η δυναμική ενέργεια ταλάντωσης είναι ίση με την κινητική του. Το συσσωμάτωμα που δημιουργείται ξεκινά μια νέα α.α.τ με πλάτος Α₂. Η απομάκρυνση του Μ στη θέση της σύγκρουσης είναι θετική και πριν τη σύγκρουση κινούνταν προς τη θετική ακραία θέση, αντίθετα από το m.

Α. Να προσδιορίσετε:

Α1. Το ρυθμό μεταβολής του μήκους του ελατηρίου ελάχιστα ... 

Συνέχεια ... 

5. Όπου με κατάλληλη ταχύτητα του ενός σώματος έχουμε τις ελάχιστες δυνατές απώλειες ενέργειας

Σώμα μάζας M = 1 kgr βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και είναι προσδεμένο στην άκρη οριζόντιου ελατηρίου σταθεράς  k  = 100 Ν/m, η άλλη άκρη του οποίου είναι στερεωμένη ακλόνητα. 

  Θέτουμε το σώμα σε α.α.τ. πλάτους  A₁ = 1 m.  Ένα βλήμα μάζας m = 0,08 kgr,  που κινείται στη διεύθυνση του άξονα του ελατηρίου με ταχύτητα υ₁, συγκρούεται πλαστικά με το σώμα, τη στιγμή που αυτό βρίσκεται  στη θέση x = -0,6 m, κινούμενο με ταχύτητα υ προς την αρνητική ακραία θέση. Μετά την κρούση το συσσωμάτωμα κάνει α.α.τ. με πλάτος Α΄= 1,2 m.

Να υπολογίσετε:  ....

Συνέχεια ...

ΣΤΑΘΕΡΗ ΔΥΝΑΜΗ ΣΕ ΣΥΣΤΗΜΑ ΟΡΙΖΟΝΤΙΟ ΕΛΑΤΗΡΙΟ-ΜΑΖΑ

Το σώμα, μάζας m = 1 kgr, αρχικά ηρεμεί στη θέση Φ όπου το ελατήριο έχει το φυσικό του μήκος. Κάποια στιγμή, που τη θεωρούμε αρχή μέτρησης των χρόνων (t = 0), αρχίζει να ενεργεί πάνω του μια σταθερή οριζόντια δύναμη F=10 Ν, που ο φορέας της ταυτίζεται με τον άξονα του ελατηρίου. 

A.  Να δείξετε ότι με την επίδραση της F το σώμα θα κάνει απλή αρμονική ταλάντωση.

 Αν τη στιγμή t₁ το σώμα σταματάει για πρώτη φορά και η δύναμη, μέσω του έργου της, έχει προσφέρει στο σύστημα ελατήριο-σώμα ενέργεια Ε=2J, να βρείτε:

Β. Το πλάτος, τη σταθερά επαναφοράς της ταλάντωσης και τη στιγμή t₁.

Γ.  Τη στιγμή t₁ καταργούμε τη δύναμη F. Να βρείτε τη χρονική στιγμή t₂  που το σώμα θα επανέλθει για πρώτη φορά στην αρχική του θέση Φ.                  

Δ. Να γραφούν οι εξισώσεις απομάκρυνσης – χρόνου, από την αρχική θέση Φ :

i. Με την F,    

ii. Χωρίς την F.                                                       

Να θεωρήσετε ως θετική φορά τη φορά της F.

ΣΥΝΟΠΤΙΚΗ ΛΥΣΗ ΚΑΙ ΠΑΡΑΤΗΡΗΣΕΙΣ

ΜΙΑ ΕΥΚΟΛΗ ΑΣΚΗΣΗ ΚΑΙ ΜΙΑ «ΕΠΙΚΙΝΔΥΝΗ» ΠΑΡΑΛΛΑΓΗ ΤΗΣ

• Α. Η άσκηση

Ένα σώμα μάζας 1 kg ηρεμεί σε λείο οριζόντιο δάπεδο στη θέση Ο, δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράς k=100 Ν/m. Το άλλο άκρο του ελατηρίου είναι σταθερά στερεωμένο σε ακλόνητο στήριγμα. Κάποια στιγμή, που τη θεωρούμε αρχή μέτρησης του χρόνου (t = 0), ασκούμε στο σώμα μια σταθερή οριζόντια δύναμη μέτρου F₀ =10 Ν, όπως στο σχήμα, οπότε αρχίζει να ολισθαίνει κατά μήκος του ημιάξονα Οx.
α. Να αποδείξετε ότι το σώμα θα εκτελέσει α.α.τ. και να προσδιορίσετε τη σχέση της μετατόπισής του από τη θέση Ο σε συνάρτηση με το χρόνο. (Θεωρείστε την προς τα δεξιά κατεύθυνση ως θετική και x = 0 στο θέση Ο).
β. Να βρείτε την εξίσωση της επιτάχυνσης του σώματος σε συνάρτηση με τη θέση του και να κάνετε τη γραφική της παράσταση.

• Δείτε την απάντηση 

•  
  Β. Η «επικίνδυνη» παραλλαγή της

Ένα σώμα μάζας m ηρεμεί αρχικά στη θέση Ο του άξονα xOx΄. Με τη βοήθεια κατάλληλου μηχανισμού αρχίζει, τη στιγμή t = 0, να κινείται προς τη θετική κατεύθυνση του άξονα με επιτάχυνση α = α₀ – βx, όπου α₀ και β γνωστές σταθερές ποσότητες και x η απόστασή  του από την αρχή Ο.

α. Να αποδείξετε ότι το σώμα θα κάνει α.α.τ.

β. Να προσδιορίσετε τις ακραίες θέσεις και τη θέση ισορροπίας της  ταλάντωσης.

 γ. Πόση είναι η μέγιστη ταχύτητα και η ενέργεια της ταλάντωσης του σώματος;

 δ. Ποια χρονική στιγμή το σώμα θα σταματήσει για πρώτη φορά; 

ΑΠΩΛΕΙΑ ΕΠΑΦΗΣ «ΑΠΟ ΤΗΝ ΑΝΑΠΟΔΗ»

• Απώλεια επαφής δύο σωμάτων, που το ένα είναι δεμένο σε ελατήριο θα συμβεί, ο κόσμος να χαλάσει, στη θέση όπου το ελατήριο αποκτά το φυσικό του μήκος. Εκεί, η ΣF σε κάθε σώμα είναι ίση με το βάρος του και η επιτάχυνση ίση με g.

Το σώμα Σ₂ του σχήματος είναι δεμένο στο κάτω άκρο  ενός αβαρούς σχοινιού το οποίο διέρχεται από μια  κατακόρυφη οπή του Σ₁. Το Σ₁ είναι δεμένο στο κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m. Το πάνω άκρο του ελατηρίου είναι στερεωμένο σε σταθερό σημείο. Τα δύο σώματα έχουν ίσες μάζες m₁ = m₂ = m = 1 kg και ισορροπούν ευρισκόμενα σε επαφή, χωρίς να είναι κολλημένα μεταξύ τους,  σε μια θέση όπου το ελατήριο είναι συμπιεσμένο κατά Δℓ με τη βοήθεια δύναμης F =100 N που ασκείται στο άλλο άκρο του σχοινιού.

(Στο σχήμα, τα Φ και Ι είναι δυο σημεία από τα οποία διέρχεται το κέντρο του Σ₁ όταν, αντίστοιχα, το ελατήριο έχει μηδενική παραμόρφωση και όταν τα δύο σώματα ισορροπούν).

Κάποια στιγμή το σχοινί κόβεται και τα δύο σώματα αρχίζουν να κινούνται προς τα κάτω.

Α.  Εξηγείστε γιατί η επαφή των δύο σωμάτων δεν χάνεται αμέσως, αλλά αφού πρώτα διανύσουν κάποιο διάστημα. Σε ποια θέση χάνεται η επαφή και πόσο είναι αυτό το διάστημα;

Β. Να βρεθεί το πλάτος ταλάντωσης του Σ₁ μετά το αποχωρισμό των σωμάτων.

Γ. Σε ποια θέση βρίσκεται το Σ₁ …

Δείτε:

• Ολόκληρη την Άσκηση με την απάντηση.
• Την προτεινόμενη Λύση της.

Σύστημα “κατακόρυφο ελατήριο - σώμα” και πλαστική κρούση. 5η περίπτωση

•  (Χρήση βαθμολογημένου άξονα - Επίπεδο δυσκολίας 5, «ψυχραιμία!»)
• Το συσσωμάτωμα ξεκινά ταλάντωση με αρχική φάση 3π/2  

Στο πάνω άκρο ενός κατακόρυφου ελατηρίου σταθεράς k = 400 Ν/m είναι στερεωμένο και ισορροπεί στη θέση Ι ένα σώμα μάζας Μ = 1 kgr (σχήμα α).       Το κάτω άκρο του ελατηρίου είναι μόνιμα στερεωμένο στο έδαφος.

 Απομακρύνουμε το σώμα κατακόρυφα προς τα κάτω κατά d = 0,1√ 2 m, ως τη θέση Β (σχήμα β) και το αφήνουμε ελεύθερο χωρίς αρχική ταχύτητα, οπότε ξεκινά να κάνει α.α.τ.

 Ένα δεύτερο σώμα ίδιας μάζας m = 3 kgr  κινείται κατακόρυφα προς τα κάτω και στην πορεία  του συναντάει το ταλαντευόμενο σώμα στη θέση x₁ = -0,1 m κάτω από τη θέση ισορροπίας του με ταχύτητα υ₀  (σχήμα γ) και συγκρούεται πλαστικά με αυτό.

Μετά την κρούση το συσσωμάτωμα που προέκυψε ξεκινάει, χωρίς αρχική ταχύτητα, μια α.α.τ. (σχήμα δ).

Α. Να υπολογίσετε ….

     Δείτε:

• Ολόκληρη την άσκηση με τις απαντήσεις.
• Την προτεινόμενη λύση.

Σύστημα “κατακόρυφο ελατήριο - σώμα” και πλαστική κρούση

• 4η περίπτωση: (Επίπεδο δυσκολίας 4, «όχι και τόσο φοβερή!»)
• ΟΠΟΥ Το συσσωμάτωμα ξεκινά ταλάντωση με αρχική φάση π και τετραπλάσια ενέργεια

 
Στο πάνω άκρο ενός κατακόρυφου ελατηρίου σταθεράς k είναι στερεωμένο και ισορροπεί στη θέση Ι ένα σώμα Σ₁ μάζας Μ = 1 kgr (σχήμα α). Το κάτω άκρο είναι στερεωμένο στο έδαφος.

Ανεβάζουμε το σώμα ως τη θέση Φ, όπου το ελατήριο έχει μηδενική παραμόρφωση, (σχήμα β) και το αφήνουμε ελεύθερο να πέσει με μηδενική αρχική ταχύτητα. Το σώμα αρχίζει να κάνει α.α.τ. (σχήμα γ).

Ένα δεύτερο σώμα Σ₂ μάζας m κινείται κατακόρυφα προς τα κάτω και στην πορεία  του συναντάει το Σ₁ στην κάτω ακραία θέση του με ταχύτητα υ₀  (σχήμα δ) και συγκρούεται πλαστικά με αυτό.

Κατά την κρούση μετατρέπεται σε θερμότητα το 50% της κινητικής ενέργειας που είχε το σύστημα αμέσως πριν την κρούση.

Μετά την κρούση (που θεωρούμε ότι συμβαίνει τη στιγμή t=0) το συσσωμάτωμα που προέκυψε ξεκινάει μια α.α.τ. με γωνιακή συχνότητα ω = 10 r/s και ενέργεια ταλάντωσης τετραπλάσια της αντίστοιχης του Σ₁ πριν την κρούση.

Να υπολογίσετε: ....

• Η συνέχεια εδώ, και
• Η Λύση εδώ

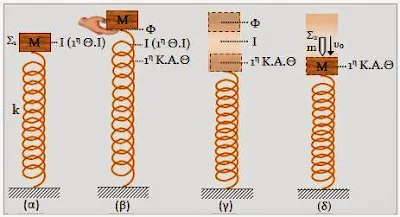
Σύστημα “κατακόρυφο ελατήριο - σώμα” και πλαστική κρούση 3η περίπτωση:

•  (Επίπεδο δυσκολίας 3, +μια απορία!)
• ΟΠΟΥ Tο συσσωμάτωμα ξεκινά ταλάντωση με αρχική φάση Π/2. (ΤΑΛΑΝΤΩΣΗ ΣΥΣΤΗΜΑΤΟΣ ΕΠΕΙΤΑ ΑΠΟ ΟΛΙΚΗ ΑΠΩΛΕΙΑ ΤΗΣ ΚΙΝΗΤΙΚΗΣ ΤΟΥ ΕΝΕΡΓΕΙΑΣ)

Το σώμα Σ₁ μάζας Μ = 1 kgr ισορροπεί στερεωμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου (σχήμα α). Το τραβάμε προς τα κάτω και κάποια στιγμή το αφήνουμε ελεύθερο χωρίς αρχική ταχύτητα (σχήμα β). Το σώμα τότε ξεκινάει μια απλή αρμονική ταλάντωση (σχήμα γ) με τα εξής χαρακτηριστικά:

1. Ο ελάχιστος χρόνος μετάβασης από τη μία ακραία θέση στην άλλη είναι 0,1π sec.

2. Η πάνω ακραία θέση είναι η Φ, όπου η παραμόρφωση του ελατηρίου είναι μηδέν.

Α. Να βρείτε τη σταθερά k του ελατηρίου και το πλάτος της ταλάντωσης του Σ₁.

    Κάποια στιγμή καθώς το σώμα Σ₁ διέρχεται από τη θέση ισορροπίας του, προσπίπτει πάνω του και συγκολλιέται με αυτό, ένα άλλο σώμα Σ₂ μάζας m που κινείται προς τα πάνω κατακόρυφα στην προέκταση του άξονα του ελατηρίου με ταχύτητα υ₀ τέτοια, ώστε το συσσωμάτωμα που δημιουργείται να έχει αμέσως μετά την κρούση ταχύτητα μηδέν.

Β.  Αν η ενέργεια ταλάντωσης του συσσωματώματος  είναι ίση με 64% της αρχικής ενέργειας ταλάντωσης του Σ₁, να βρείτε τη μάζα m του Σ₂.

Γ. Εξηγείστε γιατί το υπόλοιπο 36% της αρχικής ενέργειας ταλάντωσης του Σ₁, δεν .......

• Ολόκληρη η άσκηση εδώ, και
• Η Λύση εδώ.