ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 2012, ΤΑ ΘΕΜΑΤΑ ΚΑΙ ΟΙ ΑΠΑΝΤΗΣΕΙΣ

ΤΑ ΘΕΜΑΤΑ

• ΓΙΑ ΤΑ ΗΜΕΡΗΣΙΑ (Εδώ)
• ΓΙΑ ΤΑ ΕΣΠΕΡΙΝΑ  (Εδώ)

ΟΙ ΣΥΝΑΔΕΛΦΟΙ ΤΟΥ Ylikonet ΣΧΟΛΙΑΖΟΥΝ ΤΑ ΘΕΜΑΤΑ

• ΤΩΝ ΗΜΕΡΗΣΙΩΝ (Εδώ)
• ΤΩΝ ΕΣΠΕΡΙΝΩΝ (Εδώ), (Εδώ) και (Εδώ)

ΟΙ ΑΠΑΝΤΗΣΕΙΣ

• ΓΙΑ ΤΑ ΗΜΕΡΗΣΙΑ (1), (2), (3), (4), (5), (6), (7)
• ΓΙΑ ΤΑ ΕΣΠΕΡΙΝΑ (1), (2)

Το αίσθημα δικαίου στους νέους πρέπει να τονωθεί

Η επιτροπή επιλογής θεμάτων τοποθέτησε φέτος ψηλά τον πήχη χωρίς ούτε το Υπουργείο αλλά ούτε και εμείς ως δάσκαλοι, οι «κύριοι», όπως με σεβασμό μας αποκαλούν οι μαθητές μας, να έχουμε δώσει ανάλογα δείγματα γραφής. 

Πού έχει δει ο μαθητής ότι η θέση μεγιστοποίησης της γωνιακής ταχύτητας, στο Γ4, είναι εκείνη όπου Στ = 0; (η στροφική ταλάντωση δεν είναι στην ύλη του). Από τις λύσεις των συναδέλφων, που παρατίθενται για αντιπαραβολή, αντιλαμβάνεται κανείς και το μέγεθος της δυσκολίας του Δ4. Η λύση μάλιστα που προτείνεται από μια ολόκληρη επιτροπή της ένωσης ελλήνων φυσικών είναι ελλιπής αφενός γιατί έχει παραλείψει την απόδειξη ότι Α΄ = 0,2 m, αφετέρου γιατί  απουσιάζει η συνάρτηση  Τ_στ = f(x). 

Ο προσδιορισμός της συνάρτησης μιας δύναμης επαφής στην ταλάντωση είναι πολύ δύσκολη υπόθεση και απαιτεί ιδιαίτερη εξοικείωση με το θέμα αυτό. Χρειάζεται μια ολόκληρη διδακτική ώρα για να συζητηθεί με τους μαθητές και ένας αριθμός εφαρμογών για να εμπεδωθεί η τεχνική. Πολλοί από εμάς το θεωρούμε υπερβολικό να αφιερώσουμε τόσο χρόνο για αυτή τη λεπτομέρεια, τη στιγμή μάλιστα που τρέχουμε για να προλάβουμε να πούμε αυτά που θεωρούμε πιο βασικά.

Θυμάμαι, εκεί στο 2001 στις τελευταίες εξετάσεις με τη μέθοδο των δεσμών, που οι μαθητές μπορούσαν να δίνουν και να ξαναδίνουν μεμονωμένα τα μαθήματα δέσμης. Είχε πέσει άσκηση με απώλεια επαφής σε κατακόρυφη ταλάντωση. Οι μαθητές τότε διδάσκονταν 5 ώρες φυσική δέσμης τη βδομάδα και τη χρονιά εκείνη όλοι οι υποψήφιοι την ξανάδιναν για 2η φορά τουλάχιστον. Κι όμως υπήρχε μεγάλη αποτυχία! Ας μη γίνω μάντης κακών για το φετινό διαγώνισμα Φυσικής.

Καλό θα ήταν τα θέματα που επιλέγονται, να μην απαιτούν εμπειρία δυσανάλογη αυτής που έχουν αποκτήσει οι μαθητές. Να μη λησμονούμε ότι εμείς τους διδάξαμε και ότι οφείλουμε να τους εξετάσουμε σε αυτά που προλάβαμε να διδάξουμε στον περιορισμένο χρόνο που το αναλυτικό πρόγραμμα προβλέπει. Τα θέματα των εξετάσεων πρέπει να επιλέγονται έτσι ώστε να επιβραβεύεται το μεγαλύτερο ποσοστό των μαθητών που οι γνώσεις και η εμπειρία τους έχουν προκύψει από την εξάσκησή τους με το υλικό που τους προσφέρει το σχολικό τους βιβλίο. (Για παράδειγμα το Δ.3, που θεωρήθηκε κι αυτό δύσκολο, ο διαβασμένος μαθητής θα το έχει δουλέψει στην άσκηση 1.40.β σελ. 38 του σχολικού). Αν ο μαθητής γνωρίζει ότι τα θέματα θα μοιάζουν με του σχολικού βιβλίου θα έχει τουλάχιστον ένα μπούσουλα. Θα τα δει, θα τα ξαναδεί, θα δει διάφορες παραλλαγές τους, θα μάθει να εμβαθύνει, θα εξασκηθεί, χωρίς να χαθεί μέσα στο χάος των άπειρων περιπτώσεων που δεν αναφέρονται στο βιβλίο. Και είναι το χάος αυτό που προκαλεί ένα τεράστιο άγχος.

 Από την εμπειρία μας γνωρίζουμε ότι με κάποιες παραλλαγές των ασκήσεων του σχολικού βιβλίου μπορούμε να φτιάξουμε διαγωνίσματα με μικρή έως και έντονη διαβάθμιση δυσκολίας. Δεν είναι απλό, αλλά για τον καλό εκπαιδευτικό είναι μια πρόκληση και είναι ο καλύτερος τρόπος να ελεγχθούν οι μαθητές. Δεν είναι τυχαίο ότι τα θέματα εξετάσεων σε κολέγια του εξωτερικού, που βρίσκουμε στο διαδίκτυο, είναι στο παραπάνω πνεύμα.

Το αίσθημα δικαίου στους νέους πρέπει να τονωθεί. Πρέπει από τις πρώτες στιγμές που μπαίνουν στον κοινωνικό στίβο να τους γίνει σαφές ότι αν προσπαθήσουν θα μπορέσουν με σιγουριά να διεκδικήσουν μια επιτυχία. Για εισαγωγικές εξετάσεις πρόκειται, όχι για διαγωνισμό ταλέντων φυσικής, μαθηματικών κ.λπ. 

Να σκεφτούμε όλοι μας τις αντίξοες συνθήκες κάτω από τις οποίες προετοιμάστηκαν τα παιδιά αυτά. Ως βαθμολογητές ας τιμήσουμε το εκπαιδευτικό μας λειτούργημα, κάνοντας το απολύτως ελάχιστο, ας προσπαθήσουμε να είμαστε δίκαιοι. 

ΠΑΙΧΝΙΔΙΑ ΜΕ ΤΗΝ 1η ΠΥΘΑΓΟΡΕΙΟ ΤΡΙΑΔΑ (3,4,5)

1. Όταν λείπει η βαρύτητα κάποια πράγματα είναι πιο απλά

Το σύστημα των αβαρών ράβδων του σχήματος έχει στο ένα άκρο του στερεωμένο ένα σφαιρίδιο αμελητέων διαστάσεων και μπορεί να περιστρέφεται χωρίς τριβές  γύρω από την άρθρωση Ο. 

Η δύναμη F ενεργεί συνεχώς κάθετα στη ράβδο του σχήματος. Αγνοώντας τη βαρύτητα, να υπολογίσετε:

Α. Το μέτρο της στροφορμής του συστήματος ως προς την άρθρωση Ο τη χρονική στιγμή t = 2 sec, θεωρώντας ότι τη στιγμή t = 0 η ταχύτητά του είναι μηδέν.

Β. Τη γωνιακή επιτάχυνση με την οποία στρέφεται το σύστημα των αβαρών ράβδων και του σφαιριδίου. 

Δείτε:

• Την άσκηση με τις απαντήσεις
• Την προτεινόμενη λύση

2. Ανάρτηση ράβδου με σχοινί

Μια ομογενής ράβδος, μήκους L = 0,6 m και μάζας m = 1 kgr, μπορεί να περιστρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το άκρο της Α. Αρχικά ηρεμεί σε κατακόρυφη θέση, όπως τη βλέπουμε στο πλαϊνό σχήμα.

Κάποια στιγμή ασκούμε στο ελεύθερο άκρο του σχοινιού μια δύναμη  F = 5 Ν.

Να βρείτε:

Α. Τον αρχικό ρυθμό μεταβολής της στροφορμής της ράβδου.

Β. Την αρχική γωνιακή επιτάχυνση της ράβδου.

Δίνεται η ροπή αδράνειας της ράβδου ως προς άξονα που είναι κάθετος στο κέντρο μάζας της Ι_c.m = mL²/12. 

Δείτε:

• Την άσκηση με τις απαντήσεις 
• Την προτεινόμενη λύση

ΤΡΟΧΟΙ ΚΑΙ … ΣΧΟΙΝΙΑ

1. Κύλιση σε λείο οριζόντιο επίπεδο

(Κι αν σας έλεγαν ότι ένας τροχός μπορεί, σε ένα εντελώς γλιστερό δρόμο, να κυλίεται χωρίς να γλιστράει ακόμη κι όταν επιταχύνεται, ακόμη κι όταν φρενάρει;)

Ο κυλινδρικός τροχός του σχήματος, ακτίνας R = 0,2 m, διαθέτει μια κεντρική εγκοπή ακτίνας r γύρω από την οποία είναι τυλιγμένο ένα λεπτό νήμα. Αρχικά ο τροχός είναι ακίνητος πάνω σε λείο οριζόντιο δάπεδο. Τραβάμε οριζόντια το άκρο Α του νήματος με δύναμη F = 10 Ν και θέτουμε τον τροχό σε κίνηση.

Α. Να δείξετε ότι για μια ορισμένη τιμή της ακτίνας r, ανεξάρτητη από την τιμή της F και της επιτάχυνσης του κέντρου μάζας, ο κύλινδρος είναι δυνατόν να κυλίεται χωρίς να ολισθαίνει.

Β.  Αν η ακτίνα r έχει την τιμή που υπολογίσατε πιο πριν, τότε:

1. Να υπολογίσετε το έργο που παράγεται από την F σε κάθε ...

Δείτε:

• Ολόκληρη την άσκηση (με τις απαντήσεις)
• Τη λύση που προτείνεται σε κάθε ερώτηση

2. Μην κάνετε το λάθος να πείτε ότι ο τροχός θα πάει προς τ ’αριστερά!

A. Πάνω σε οριζόντιο δάπεδο μπορεί να κυλάει ένας κυλινδρικός τροχός ακτίνας R = 0,2 m. Στο μέσον του υπάρχει ένα στενό βαθύ αυλάκι ακτίνας r = 0,1 m γύρω από το οποίο είναι τυλιγμένο ένα λεπτό νήμα που το άκρο του Α το τραβάμε προς τα δεξιά με ταχύτητα υ_Α  = 0,5 m/s.

Να βρείτε τη γωνιακή ταχύτητα περιστροφής του κυλίνδρου θεωρώντας ότι κυλίεται χωρίς να ολισθαίνει. 
  

Β. Ακινητοποιούμε τον τροχό κι επαναλαμβάνουμε το πείραμα ασκώντας στο άκρο Α του σχοινιού σταθερή οριζόντια δύναμη F = 10 N. Να δείξετε ότι το έργο της F σε κάθε περιστροφή του τροχού είναι σταθερό και να υπολογίσετε. 

   

Δείτε:

• Την άσκηση με την απάντηση (σε PDF)
• Την προτεινόμενη λύση.

ΡΑΒΔΟΣ ΚΑΙ ΤΡΟΧΟΣ ΣΤΟ ΕΣΩΤΕΡΙΚΟ ΚΥΛΙΝΔΡΙΚΗΣ ΕΠΙΦΑΝΕΙΑΣ

Ο τροχός αποτελείται από ένα στεφάνι μάζας 4 kgr ακτίνας 0,25 m το οποίο μπορεί να περιστρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο του Κ, με τη βοήθεια μεταλλικών ακτίνων αμελητέας μάζας. Ο άξονας του τροχού προσαρτάται στην οριζόντια ράβδο ΟΚ μάζας m = 3 kgr που το άκρο της Ο είναι αρθρωμένο σε ακλόνητο στήριγμα. Αν το σύστημα αφήνεται από την ηρεμία με τη ράβδο αρχικά οριζόντια, όπως φαίνεται στο σχήμα  και αν ο τροχός κυλίεται στην κυλινδρική επιφάνεια χωρίς να ολισθαίνει, να υπολογίσετε την ταχύτητα του κέντρο Κ του τροχού όταν φτάνει στην κατώτερη θέση Κ΄.

Δίνονται: OK = R = 0,5 m, ΟC = 0,3 m,  I_{ράβδου(Ο)} = 0,32 kgr.m² και g = 10 m/s² και ότι η μάζα του τροχού είναι συγκεντρωμένη στην περιφέρειά του. Οι τριβές στο άξονα περιστροφής και στην άρθρωση είναι αμελητέες.

Δείτε:

• Την άσκηση σε PDF (με την απάντηση)
• Την προτεινόμενη λύση της

ΜΕΤΑΦΟΡΙΚΗ, ΣΤΡΟΦΙΚΗ ΚΑΙ ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ ΣΥΣΤΗΜΑΤΟΣ ΣΤΕΡΕΩΝ

 To σύστημα του σχήματος αποτελείται από το σώμα Σ με m_Σ = 8kg, την τροχαλία Π₁ και τον τροχό Π₂ με μάζες m₁ = 1kg, m₂ = 4kg και ακτίνες R₁ = 0,1 m, R₂ = 0,2 m, αντίστοιχα.
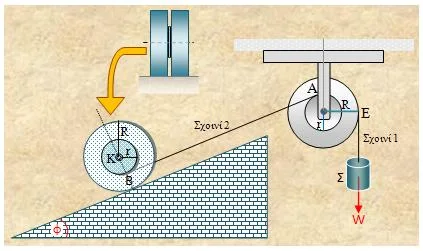
Αν γνωρίζετε ότι το σύστημα των τριών σωμάτων τίθεται σε κίνηση τη στιγμή t = 0 με το Σ να ολισθαίνει προς τα κάτω, ότι ο τροχός Π₂ κυλίεται χωρίς να ολισθαίνει προς τα επάνω, και η τροχαλία Π₁ στρέφεται χωρίς τριβές γύρω από σταθερό άξονα με το νήμα να μην ολισθαίνει στην περιφέρεια της, να μελετήσετε την κίνηση του συστήματος απαντώντας στα παρακάτω ερωτήματα:
Α.  Να βρείτε την επιτάχυνση α_Σ του σώματος Σ, εάν την χρονική στιγμή t₁ = 2s o τροχός Π₂ έχει εκτελέσει  5/π περιστροφές. 
Β. Να υπολογίσετε τις τάσεις των νημάτων καθώς και τη στατική τριβή που αναπτύσσεται μεταξύ του δαπέδου και του τροχού.
Γ. Να υπολογίσετε τις στροφορμές της τροχαλίας Π₁ και του τροχού Π₂ όταν το σώμα Σ έχει μετατοπιστεί κατακόρυφα ...

Δείτε:

• Ολόκληρη την άσκηση (με τις απαντήσεις)
• Την προτεινόμενη λύση της

ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ

Στάσιμο κύμα, με στοιχεία ταλάντωσης, σε χορδή συγκεκριμένου μήκους  

Μια τεντωμένη οριζόντια χορδή ΟΑ μήκους L εκτείνεται κατά τη διεύθυνση του άξονα x. Το άκρο Α είναι ακλόνητα στερεωμένο, ενώ το άκρο Ο που βρίσκεται στη θέση x = 0 είναι ελεύθερο, έτσι ώστε με κατάλληλη διαδικασία να δημιουργείται στάσιμο κύμα. Στη θέση x = 0 εμφανίζεται κοιλία και το υλικό σημείο του μέσου στη θέση αυτή εκτελεί απλή αρμονική ταλάντωση. Τη χρονική στιγμή t = 0 το σημείο x = 0 βρίσκεται στη θέση μηδενικής απομάκρυνσης κινούμενο κατά τη θετική φορά. Στο σχήμα απεικονίζεται το στιγμιότυπο του συγκεκριμένου στάσιμου κύματος τη στιγμή κατά την οποία όλα τα σημεία της χορδής βρίσκονται στις θέσεις μέγιστης απομάκρυνσής τους. Η μέγιστη απόσταση μεταξύ της πρώτης κοιλίας και του δεύτερου δεσμού είναι 0,1√ 10 m. Ο ελάχιστος χρόνος που χρειάζεται κάθε υλικό σημείο του ελαστικού μέσου που ταλαντώνεται, για να διέλθει δύο φορές από τη θέση ψ₁ =|A΄|/2 είναι Δt =1/60 sec, όπου |Α΄| είναι το πλάτος της ταλάντωσης του σημείου.

Α.  Να γραφεί η εξίσωση του στάσιμου κύματος.

Β.  Να βρεθεί το μέτρο της ταχύτητας και το μέτρο της επιτάχυνσης μιας κοιλίας, όταν έχει απομάκρυνση  ψ₁ = 6.10^-2 m.

Γ.  Να υπολογιστεί το μήκος της χορδής, εάν στο στάσιμο κύμα έχουν δημιουργηθεί οκτώ  δεσμοί  (συμπεριλαμβανομένου και του δεσμού στο άκρο Α).

Δ.  Εάν η συχνότητα των κυμάτων που δημιουργούν το στάσιμο κύμα γίνει  f = 20/3 Hz να βρεθεί ο αριθμός των δεσμών που σχηματίζονται στην ίδια χορδή, με δεδομένο ότι στην αρχή της χορδής έχουμε πάλι κοιλία και στο τέλος δεσμό. Δίνεται π² = 10.

Δείτε:

• Την άσκηση σε PDF (με τις απαντήσεις)
• Την προτεινόμενη λύση της 

Δυο σώματα, δύο ελατήρια, μια πλαστική κρούση και ένα κύμα

Οι σταθερές των δύο ελατηρίων του σχήματος είναι k₁= 100 N/m και k₂ = 300 N/m, ενώ οι μάζες των σωμάτων Σ₁ και Σ₂ είναι m₁ = 1 kgr και m₂ = 3 kgr, αντίστοιχα.

 Αρχικά, τα σώματα Σ₁ και Σ₂ ισορροπούν εφαπτόμενα στη θέση Ι χωρίς να ασκούν δύναμη το ένα στο άλλο. Στο Σ₁ είναι στερεωμένο ένα τεντωμένο οριζόντιο σχοινί Οx μεγάλου μήκους. Η ακλόνητα στηριγμένη κατακόρυφη ράβδος ΑΒ και οι δακτύλιοι δ₁ και δ₂ που είναι περασμένοι σ’ αυτήν και είναι στερεωμένοι στα σώματα, χρησιμεύουν στο να εξουδετερώνεται η τάση του σχοινιού και οι άξονες των δύο ελατηρίων να διατηρούνται κατακόρυφοι.

Απομακρύνουμε προς τα κάτω το Σ₂ κατά 20 cm και το αφήνουμε ελεύθερο να κινηθεί. Ανέρχεται, και στη θέση Ι συγκρούεται πλαστικά με το Σ₁. Το συσσωμάτωμα που προκύπτει αρχίζει να ταλαντώνεται παρασύροντας το άκρο Ο του σχοινιού σε μια παρόμοια κίνηση. Έτσι, πάνω στο σχοινί ξεκινάει η διάδοση ενός εγκάρσιου κύματος με ταχύτητα 10 cm/s.

Α. Να αποδείξετε η ταλάντωση του συσσωματώματος είναι απλή αρμονική με σταθερά επαναφοράς  D = k₁ + k₂ .

Β. Να υπολογίσετε το πλάτος της ταλάντωσης του συσσωματώματος και να γράψετε τη σχέση της απομάκρυνσής του σε συνάρτηση με το χρόνο.

Γ. Να υπολογίσετε το μήκος κύματος λ …

Δείτε:

·         Ολόκληρη την άσκηση με τις απαντήσεις

·         Τη λύση της 

ΤΑΛΑΝΤΩΣΗ ΣΤΗΝ ΚΑΤΑΚΟΡΥΦΗ ΔΙΕΥΘΥΝΣΗ ΚΑΙ ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ

 Πώς μια κρούση στην κατάλληλη θέση καθιστά το πλάτος ταλάντωσης μέγιστο.  

Το πάνω άκρο ενός κατακόρυφου ελατηρίου έχει στερεωθεί στην οροφή ενός δωματίου, ενώ στο κάτω άκρο του έχει προσδεθεί σφαιρικό σώμα Σ₁ μάζας m.  

   Υποβαστάζουμε το σώμα ώστε το ελατήριο να έχει το φυσικό του μήκος ℓ₀, και κάποια στιγμή το αφήνουμε ελεύθερο. Το σώμα Σ₁ αρχίζει να εκτελεί απλή αρμονική ταλάντωση. Παρατηρούμε ότι το χαμηλότερο σημείο στο οποίο φτάνει, απέχει από το σημείο που το αφήσαμε 20 cm.

Α.  Υπολογίστε τη συχνότητα της ταλάντωσης και το μέτρο της ταχύτητας του σώματος όταν περνάει από τη θέση που βρίσκεται 10 cm πιο κάτω από τη θέση που το αφήσαμε. Δίνεται: g = 10 m/sec².

Β. Κάτω από το Σ₁ και σε απόσταση h = 50 cm από τη θέση που το αφήνουμε ελεύθερο να ταλαντωθεί,  βρίσκεται ένα άλλο σφαιρικό σώμα Σ₂ ίδιας μάζας με το Σ₁. Το κέντρο του Σ₂ βρίσκεται πάνω στην κατακόρυφο που ταλαντώνεται το κέντρο του Σ₁. Κάποια στιγμή το Σ₂ βάλλεται προς τα πάνω με αρχική ταχύτητα υ₀ = 3 m/sec και συγκρούεται κεντρικά κι ελαστικά με το Σ₁. Σε ποια θέση πρέπει να βρίσκεται το Σ₁ τη στιγμή της κρούσης, ώστε μετά από αυτή, το πλάτος της ταλάντωσής του να είναι το μέγιστο δυνατό; Δικαιολογείστε την απάντησή σας.

Γ. Πόσο είναι .... 

                                                                          

Δείτε:

• Ολόκληρη την άσκηση (με τις απαντήσεις
• 
  
• Την προτεινόμενη λύση

ΑΝΕΒΑΙΝΕΙ Ή ΚΑΤΕΒΑΙΝΕΙ;

Το σώμα Σ του πλαϊνού σχήματος είναι δεμένο στο άκρο ενός λεπτού αβαρούς σχοινιού (σχοινί 1) τυλιγμένου στο περιμετρικό αυλάκι μιας τροχαλίας η οποία  μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από ακλόνητο οριζόντιο άξονα. Στην ίδια τροχαλία υπάρχει και ένα άλλο αυλάκι, ομοαξονικό με το πρώτο, με ακτίνα r = R/2, στο οποίο είναι τυλιγμένο το σχοινί 2.

Η άλλη μεριά αυτού του σχοινιού είναι τυλιγμένη γύρω από μια κεντρική εγκοπή ενός κυλινδρικού τροχού που μπορεί να κυλίεται πάνω σε ένα πλάγιο επίπεδο χωρίς να ολισθαίνει, όπως στο σχήμα. Οι ακτίνες της εγκοπής του τροχού και της περιφέρειάς του είναι, αντίστοιχα, r και R, ίσες με τις ακτίνες των δύο αυλακιών της τροχαλίας.

Τη στιγμή t = 0 αφήνουμε το σύστημα ελεύθερο να κινηθεί και παρατηρούμε ότι το  σχοινί 2 τυλίγεται στο αυλάκι της τροχαλίας με τη μικρή ακτίνα. Το σώμα Σ κατέρχεται με σταθερή επιτάχυνση 1,8 m/s²,  ενώ ο κύλινδρος κυλίεται χωρίς να ολισθαίνει.

Α. Να εξετάσετε αν ο κύλινδρος ανέρχεται ή κατέρχεται στο πλάγιο επίπεδο.

Β. Να βρείτε την επιτάχυνση, την ταχύτητα και τη μετατόπιση του κυλίνδρου τη ...
 ..........................................................................................................................
Δείτε:

• Όλη την άσκηση (με απαντήσεις)
• Την προτεινόμενη λύση της